TP
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
18 tháng 4 2017
\(f\left(1\right)=2\Rightarrow a.1+b^2=2\)
\(\Rightarrow a+b^2=2\Rightarrow b^2=2-a\)
\(f\left(3\right)=8\Rightarrow a.3+b^2=8\Rightarrow3a+b^2=8\)
\(\Rightarrow3a+\left(2-a\right)=8\)
\(\Rightarrow3a+2-a=8\)
\(\Rightarrow2a=6\)
\(\Rightarrow a=3\)
Khi đó , \(b^2=2-3=-1\)
hmmm... mình có làm sai đoạn nào ko nhỉ 
. Sao tự dưng b thuộc rỗng
LT
0
NT
13 tháng 12 2017
Nếu x0 là một nghiệm của f(x) thì \(a.x_0+b=0\Rightarrow a=\dfrac{-b}{x_0}\)
Nếu \(x=\dfrac{1}{x_0}\)
\(\Rightarrow\dfrac{b}{x_0}+a=\dfrac{b}{x_0}+\left(-\dfrac{b}{x_0}\right)=0\)
=> đpcm
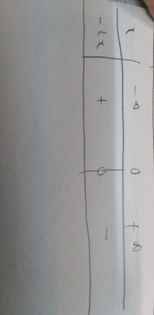
- Nhị thức \(f\left(x\right)=a\)\(x+b\left(a\ne0\right)\) cùng dấu với hệ số \(a\) khi \(x\) lấy giá trị trong khoảng \(\left(\frac{-b}{a};+\infty\right)\) và trái dấu với hệ số \(a\) khi \(x\) lấy các giá trị trong khoảng \(\left(-\infty;\frac{-b}{a}\right)\).
Nhị thức bậc nhất đối với x là biểu thức dạng f(x) = ax + b, trong đó a và b là hai số cho trước, với a ≠ 0 và a được gọi là hệ số của x hay hệ số của nhị thức.