Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tam giác A'B'C' đồng dạng với tam giác ABC với tỉ số đồng dạng \(\frac{1}{5}\)

Lời giải:
Giả sử $AB=3, AC=4, BC=5$ (cm)
Vì $3^2+4^2=5^2$ nên theo định lý Pitago đảo thì $ABC$ là tam giác vuông tại $A$
$A'B'C'$ đồng dạng với $ABC$ nên $A'B'C'$ là tam giác vuông tại $A'$
$\Rightarrow S_{A'B'C'}=\frac{A'B'.A'C'}{2}=54\Rightarrow A'B'.A'C'=108(*)$ (cm)
$ABC\sim A'B'C'\Rightarrow \frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}$
$\Leftrightarrow \frac{A'B'}{3}=\frac{B'C'}{5}=\frac{C'A'}{4}(**)$
Từ $(*); (**)$ suy ra $A'B'=9; B'C'=15; C'A'=12$ (cm)

e làm a,b chung luôn nha chị
Xét tam giác ABC và tam giác A`B`C`, có:
\(\dfrac{AB}{A`B`}=\dfrac{BC}{B`C`}=2\) ( gt )
Góc A = góc A` = 90 độ
=> tam giác ABC đồng dạng tam giác A`B`C`
=>\(\dfrac{AC}{A`C`}=\dfrac{AB}{A`B`}=\dfrac{BC}{B`C`}=2\) ( tính chất 2 tam giác đồng dạng )

Lời giải
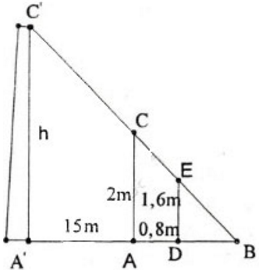
Gọi chiều cao của cây là h = A'C' và chọn một cọc tiêu AC = 2m.
Khoảng cách từ chân đến mắt người đo là DE = 1,6m.
Cọc xa cây một khoảng A'A = 15m, và người cách cọc một khoảng AD = 0,8m và gọi B là giao điểm của C'E và A'A.
Giải:
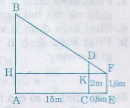
Giả sử AB là cây cần do, CD là cọc EF là khoảng cách từ mắt tới chân.
∆KDF ∽ ∆HBF
=> HBKD=HFKFHBKD=HFKF
=> HB = HF.KDKFHF.KDKF
mà HF = HK + KF =AC + CE = 15 + 0,8 = 15.8m
KD = CD - CK = CD - EF = 2 - 1,6 = 0,4 m
Do đó: HB = 7,9 m
Vậy chiều cao của cây là 7,9 m.
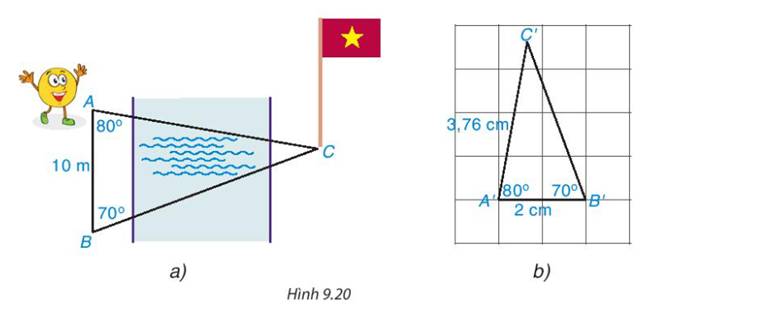

Có ΔA'B'C' ∽ ΔABC với tỉ số đồng dạng là \(\frac{1}{5}\)
\(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = \frac{1}{5}\)
mà A′C′=3,76 (m) => AC=18,8 (m)
Khoảng cách từ bạn Tròn đến chân cột cờ là 18,8 m.