
 Tết đến rồi.
Tết đến rồi.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

 Tết đến rồi.
Tết đến rồi.

a) Sơ đồ cây trong đó B là ngày có mưa và A là nhà không mưa.
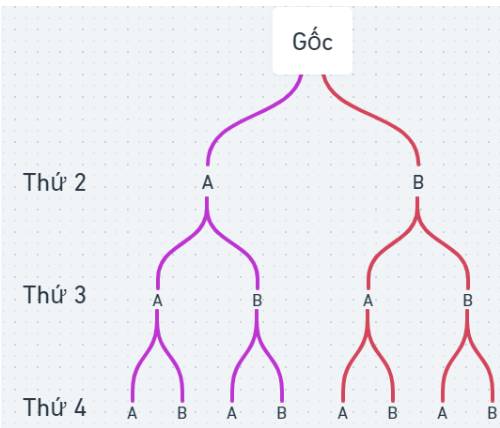
Dựa vào sơ đồ cây ta thấy \(n\left( \Omega \right) = 8\).
b) Ta có \(F = \left\{ {AAB,ABA,BAA} \right\}\). Vậy \(P\left( F \right) = \frac{3}{8}\).
\(G = \left\{ {AAB,ABA,BAA,AAA} \right\}\). Vậy \(P\left( G \right) = \frac{1}{2}\).

a) Xét: x2 - 4mx + 9.(m – 1)2 = 0 (1)
Δ’ = (2.m)2 – 9.(m – 1)2 = 4m2 – 9.(m2 – 2m + 1) = -5m2 + 18m – 9
Phương trình (1) có nghiệm ⇔ Δ’ ≥ 0
⇔ -5m2 + 18m – 9 ≥ 0
⇔ 5m2 - 18m + 9 ≤ 0
⇔ (5m – 3)(m – 3) ≤ 0
⇔ 3/5 ≤ m ≤ 3.
b) + x1 ; x2 là hai nghiệm của (1) nên theo định lý Vi-et ta có:
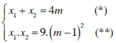
+ Tìm hệ thức giữa x1 và x2 không phụ thuộc vào m.
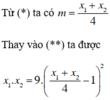
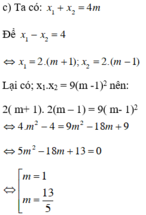
Thử lại:
+ m = 1, (1) trở thành x2 – 4x = 0 có hai nghiệm x = 0; x = 4 có hiệu bằng 4
+ m = 13/5, (1) trở thành 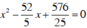 có hai nghiệm x = 7,2 và x = 3,2 có hiệu bằng 4.
có hai nghiệm x = 7,2 và x = 3,2 có hiệu bằng 4.
Vậy m = 1 hoặc m = 13/5.

Gọi x (ngày) là số ngày dự định làm xong kế hoạch (x > 0).
Khi đó:
Số sản phẩm dự định làm trong một ngày là: 360/x (sản phẩm)
Thực tế, mỗi ngày làm thêm được 9 sản phẩm nên năng suất thực tế là: 360/x + 9 (sản phẩm / ngày)
Số ngày làm thực tế là: x – 1 (ngày)
Số sản phẩm làm được trong x – 1 ngày là: 360 + 360.5% = 378 sản phẩm.
Ta có phương trình:
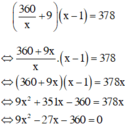
⇔ x = 8 (thỏa mãn) hoặc x = –5 (loại)
Số ngày dự định là 8 ngày, năng suất thực tế là 360:8 + 9 = 54 sản phẩm/ngày
Vậy khi đến hạn, phân xưởng sẽ làm được 54.8 = 432 sản phẩm.

Gọi x là số sản phẩm sản xuất trong một ngày theo định mức.
Điều kiện x nguyên dương. Theo đề ta có chương trình:
\(\dfrac{360}{x}=\dfrac{360+\dfrac{360.5}{100}}{x+9}+1\)
⇔ x2 + 27x – 3240 = 0
⇒ x1= -72 (loại), x2 = 45.
Thời gian giao hoàn thành kế hoạch là = 8 ngày
Nếu sản xuất theo thời gian đã định với năng suất mới thì số sản phẩm làm được là (45+9).8=432 sản phẩm.

Đổi 60g=0,06kg, 50g=0,05kg
Lượng đường cần cho x chiếc bánh nướng là 0,06x kg
Lượng đường cần cho y chiếc bánh dẻo là 0,05y kg
Vì lượng đường đã nhập về là 500kg và lượng đường sản xuất bánh không vượt quá lượng đường đã nhập về nên ta có:
\(0,06x + 0,05y \le 500\)