K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
6 tháng 2 2022
a) \(\left\{{}\begin{matrix}M=x^2y-2xy+6-xy=x^2y-3xy+6\\N=-2x^2y+2xy+x^2y-3=-x^2y+2xy-3\end{matrix}\right.\)
b) \(x=1;y=2\Rightarrow M=1^2.2-2.1.2+6-1.2=2\)
c) \(M+N\Rightarrow x^2y-3xy+6+\left(-x^2y\right)+2xy-3=-xy+3\)
SG
2
19 tháng 9 2018
M + N = \(x^2-2xy+y^2\)+\(y^2+2xy+x^2+1\)
= \(\left(x^2+x^2\right)+\left(-2xy+2xy\right)+\left(y^2+y^2\right)+1\)
= \(2x^2+2y^2+1\)
M - N = \(x^2-2xy+y^2-y^2+2xy+1\)
= \(\left(x^2+x^2\right)+\left(-2xy+2xy\right)+\left(y^2-y^2\right)+1\)
= \(2x^2+1\)
TD
1
FY
1
VN
4 tháng 4 2017
a/ M + N = x\(^2\)- 2xy + y\(^2\)+ y\(^2\)+ 2xy + x\(^2\)+ 1
= 2x\(^2\)+ 2y\(^2\)+ 1
= 2( x\(^2\)+ y\(^2\)) + 1
b/ M - N = x\(^2\)- 2xy + y\(^2\)- ( y\(^2\)+ 2xy + x\(^2\)+ 1 )
= x\(^2\)- 2xy + y\(^2\)- y\(^2\)- 2xy - x\(^2\)- 1
= -4xy - 1
MS
23 tháng 4 2018
\(M=x^2-2xy+y^2\)
\(N=y^2+2xy+x^2+1\)
\(a,M+N=\left(x^2-2xy+y^2\right)+\left(y^2+2xy+x^2+1\right)\)
\(=x^2-2xy+y^2+y^2+2xy+x^2+1\)
\(=\left(x^2+x^2\right)+\left(-2xy+2xy\right)+\left(y^2+y^2\right)+1\)
\(=2x^2+2y^2+1\)
\(b,M-N=\left(x^2-2xy+y^2\right)-\left(y^2+2xy+x^2+1\right)\)
\(=x^2-2xy+y^2-y^2-2xy-x^2-1\)
\(=\left(x^2-x^2\right)+\left(-2xy-2xy\right)+\left(y^2-y^2\right)-1\)
\(=-4xy-1\)
HH
5
HH
17 tháng 8 2016
a, M + N = \(\left(x^2-2xy+y^2\right)+\left(y^2+2xy+x^2+1\right)\)
=\(2x^2+2y^2+1\)
b,M - N =\(\left(x^2-2xy+y^2\right)-\left(y^2+2xy+x^2+1\right)\)
=\(-4xy-1\)
PQ
0
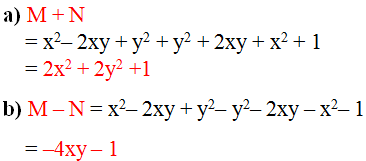
\(M+N=2x^2+2y^2+1\)
\(M-N=x^2-2xy+y^2-x^2-2xy-y^2-1=-4xy-1\)