Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đọc lại đề đi bạn, đừng có làm bừa như thế (cop bừa thì đúng hơn chứ nhỉ)
Thời gian đi nửa đoạn đường đầu:
\(t_1=\dfrac{S_1}{v_1}=\dfrac{\dfrac{1}{2}S}{v_1}=\dfrac{S}{2v_1}=\dfrac{S}{40}h\)
Thời gian đi nửa đoạn đường sau:
\(t_2=\dfrac{S_2}{v_2}=\dfrac{S}{2v_2}h\)
Vận tốc trung bình:
\(v_{tb}=\dfrac{S}{t_1+t_2}=\dfrac{S}{\dfrac{S}{40}+\dfrac{S}{2v_2}}=48\)
Suy ra v2 nhé.

Thời gian đi nửa quãng đường đầu:
\(t_1=\dfrac{S_1}{v_1}=\dfrac{\dfrac{1}{2}S}{v_1}=\dfrac{S}{2v_1}\left(h\right)\)
Thời gian đi nửa quãng đường sau:
\(t_2=\dfrac{S_2}{v_2}=\dfrac{\dfrac{1}{2}S}{v_2}=\dfrac{S}{2v_2}\left(h\right)\)
Vận tốc trung bình:
\(v_{tb}=\dfrac{S}{t_1+t_2}=\dfrac{S}{\dfrac{S}{2v_1}+\dfrac{S}{2v_2}}=\dfrac{2v_1v_2}{v_1+v_2}\) (km/h)

Giải thích các bước giải:
*đối với người đi từ M đến N
thời gian người đó đi hết nửa quãng đường đầu là
T1=0.5S/v1 =S/40 (h)
thời gian người đó đi hết nửa quãng đường còn lại là
T2=0.5S/V2=S/120 (h)
*Đối với người đi từ N đến M
quãng đường người đó đi được trong nửa giờ đầu là
S1'=0.5t'.v1=10t'(km)
Quãng đường người đó đi trong nửa giờ au là
S2'= 0.5t'.v2=30t'
Mà S1'+S2'=S
10t'+30t'=S
t'=S/40(h)
Vì nếu xe xuất phát từ N đi muộn hơn xe đi từ M 0.5h thì hai xe gặp nhau cùng một lúc nên ta có
T1+T2 =t'+0.5
S/40+s/120=s/40+0.5
S=60(km )

Gọi s là chiều dài nửa quãng đường mà người đi xe đạp phải đi.
Như vậy, thời gian đi hết nửa quãng đường đầu s1 = s với vận tốc v1 là:
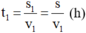
Thời gian đi hết nửa quãng đường còn lại s2 = s với vận tốc v2 là:
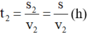
Vậy tổng thời gian đi hết cả quãng đường là: 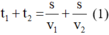
Vận tốc trung bình của người đi xe đạp trên cả quãng đường là:
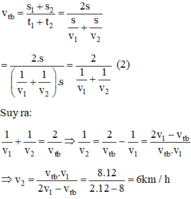

\(400m=0,4km\)
Vận tốc của xe trên nửa quãng đường còn lại là:
\(v_2=\dfrac{v_1}{2}=\dfrac{36}{2}=18\left(km/h\right)\)
Thời gian xe đi trên nửa quãng đường đầu là:
\(t_1=\dfrac{AB}{2v_1}=\dfrac{0,4}{2.36}=\dfrac{1}{180}\left(h\right)\)
Thời gian xe đi trên nửa quãng đường còn lại là:
\(t_2=\dfrac{AB}{2v_2}=\dfrac{0,4}{2.18}=\dfrac{1}{90}\left(h\right)\)
Vận tốc trung bình trên cả quãng đường AB là:
\(v_{tb}=\dfrac{AB}{t_1+t_2}=\dfrac{0,4}{\dfrac{1}{180}+\dfrac{1}{90}}=24\left(km/h\right)\)

\(=>vtb=\dfrac{S}{\dfrac{\dfrac{1}{2}S}{v1}+\dfrac{\dfrac{1}{2}S}{v2}}=\dfrac{S}{\dfrac{S}{72}+\dfrac{S}{2v2}}=24\)
\(=>\dfrac{S}{\dfrac{S\left(2v2+72\right)}{144v2}}=24=>\dfrac{144v2}{2v2+72}=24=>v2=18km/h\)

\(v_1=27\left(\dfrac{km}{h}\right)\\ s_1=27.\dfrac{1}{3}=9\left(km\right)\\ v_{tb}=54\left(\dfrac{km}{h}\right)\\ s_{AB}=9:\left(1-\dfrac{2}{3}\right)=27\left(km\right)\\ v_{tb}=\dfrac{s_1+s_2}{t_1+t_2}=\dfrac{27}{\dfrac{1}{3}+\dfrac{s_2}{v_2}}\\ \Leftrightarrow54=\dfrac{27}{\dfrac{1}{3}+\dfrac{27-9}{v_2}}\\ \Leftrightarrow v_2=108\left(\dfrac{km}{h}\right)\)

Vận tốc người đi xe đạp đi nửa quãng đường còn lại là:
vtb=2112+1v2=214=8(kmh)vtb=2112+1v2=214=8(kmh)
=> 14−112=1614−112=16 => v2=6(kmh)v2=6(kmh)
Đáp số: 6 km/h.