Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi thời gian ở quãng đường đầu và quãng đường thứ hai lần lượt là: t1( S1, V1) , t2( S2, V2)
theo bài ta có : t1=t2=1/2 t
Vtb= S1+S2/ t1+t2= 8
thay dữ liệu vào phép tính trên ta đc:
Vtb= S1+S2/ t1+t2= V1*t1 + V2*t2/ t1+t2 = 1/2t*V1 +1/2t*V2/ 1/2t+1/2t
<=> t*(1/2*V1 +1/2*V2)/ t = 1/2*12 + 1/2*V2 = 8
= 6+ 1/2* V2 = 8
= V2 = 4 (km/h)
Gọi thời gian xe đi đoạn nửa đoạn đầu và nửa đoạn sau là \(t_1\) và \(t_2\)
Thời gian xe đi nửa quãng đường đầu là: \(t_1=\frac{\frac{1}{2}S}{v_1}=\frac{S}{24}\)
Thời gian xe đi nửa quãng đường sau là: \(t_2=\frac{\frac{1}{2}S}{v_2}=\frac{S}{2v_2}\)
Vận tốc trung bình của xe là: \(v_{tb}=\frac{S}{t_1+t_2}=\frac{S}{\frac{S}{24}+\frac{S}{2v_2}}=\frac{1}{\frac{1}{24}+\frac{1}{2v_2}}=8km/h\)
\(\Rightarrow\frac{1}{24}+\frac{1}{2v_2}=\frac{1}{8}\)
\(\Rightarrow2v_2=12\)
\(\Rightarrow v_2=6km/h\)

gọi s1 = s2 = s3 = s/3
ta có : v1 = s1/t1 -> t1 = s/3.v1 = s/30
v2 = s2/t2 -> t2 = s/3.v2 = s/24
v3 = s3/t3 -> t3 = s/3.v3 = s/16
Ta có công thức vận tốc trung bình
Vtb = S/t => S/ t1+t2+t3 = S/ s/30 + s/24 + s/16
= S/ 33s/240 = 1/ 33/240 = 240/33 = 7 ( xấp xỉ )

Gọi 1/3 QĐ là S
vtb=3S/(S/v1+2S/v2)=3/(1/v1+1/v2)
40=3/(1/30+2/v2)=>v2=48km/h

gọi s là quãng đường AB
s1,s2,s3 lần lượt là từng quãng đường mà xe di chuyển:
s1 = \(\frac{1}{3}s\)
=> s2 + s3 = \(\frac{2}{3}s\)
Thời gian xe di chuyển trong \(\frac{1}{3}\) quãng đường là:
t1 = \(\frac{s_1}{v_1}=\frac{s}{3.40}=\frac{s}{120}\)
Gọi t' là thời gian đi ở quãng đường (\(\frac{2}{3}s\)) còn lại:
Trong \(\frac{2}{3}\) thời gian đầu, xe đi được quãng đường là
s2 = \(\frac{2}{3}t'.v_2=\frac{2}{3}.t'.45=30t'\)
Quãng đường xe đi được trong thời gian còn lại là:
s3=\(\frac{1}{3}t'.v_3=\frac{1}{3}t'.30=10t'\)
Mặt khác ta có
s2 + s3 = \(\frac{2}{3}s\)
=> 30t' + 10t' = \(\frac{2}{3}s\)
=> 40t'=\(\frac{2}{3}s\)
=> t'=\(\frac{s}{60}\)
Vận tốc trung bình của xe là:
\(v_{tb}=\frac{s}{t+t'}=\frac{s}{\frac{s}{120}+\frac{s}{60}}=\frac{1}{\frac{1}{120}+\frac{1}{60}}=40\)(km/h)

Một xe đi từ A về B, trong nửa quãng đương đầu, xe chuyển động với vận tốc v1= 40 km/h. Trên nửa quãng đường sau xe chuyển động thành 2 giai đoạn: nửa thời gian đầu vận tốc v2 = 45 km/h, thời gian còn lại đi với vận tốc v3 = 30 km/h. Tính vận tốc trung bình của xe trên cả quãng đường AB.
Đề phải như này mới đúng

Gọi S là chiều dài quãng đường ta có :
Thời gian đi hết nửa quãng đường đầu là :\(t_1=\frac{S}{2v_1}\)
Thời gian đ hết nửa quãng đường sau là :
\(t_2=\frac{S}{2v_2}\)
Vận tốc trung bình trên cả quãng đường S là :
\(v_{tb}=\frac{S}{\left(t_1+t_2\right)}\Rightarrow\left(t_1+t_2\right)=\frac{S}{v_{tb}}\)
Từ các điều nói trên : \(\frac{1}{v_1}+\frac{1}{v_2}=\frac{2}{v_{tb}}\)
Thế số vào tính được v2 = 7,5 km/h
ta có:
thời gian người đó đi trong nửa quãng đường đầu là:
\(t_1=\frac{S_1}{v_1}=\frac{S}{2v_1}=\frac{S}{30}\)
thời gian người đó đi trong quãng đường còn lại là:
\(t_2=\frac{S_2}{v_2}=\frac{S}{2v_2}\)
vận tốc trung bình của người đó là:
\(v_{tb}=\frac{S}{t_1+t_2}=\frac{S}{\frac{S}{30}+\frac{S}{2v_2}}=\frac{S}{S\left(\frac{1}{30}+\frac{1}{2v_2}\right)}=\frac{1}{\frac{1}{30}+\frac{1}{2v_2}}\)
\(\Leftrightarrow10=\frac{1}{\frac{v_2+15}{30v_2}}=\frac{30v_2}{v_2+15}\)
giải phương trình trên ta có:
v2=7,5km/h

gọi t là thời gian xe di chuyển đến đền hùng
t1 là thời gian đi với vận tốc v1 = 90(km/h)
t2 là thời gian xe đi với vận tốc v2 = 60 (km/h)
theo đề ta có t1 = t2 =\(\frac{1}{2}t\)
Trong nửa thời gian đi thì xe đi được quãng đường là:
s1 = v1 . t1 = 90.\(\frac{1}{2}t=45t\left(km\right)\)
Trong thời gian còn lại xe đi được quãng đường là:
s2 = v2.t2 =60.\(\frac{1}{2}t=30t\left(km\right)\)
Vận tốc trung bình xe đi trên cả quãng đường là:
vtb = \(\frac{s_1+s_2}{t_1+t_2}=\frac{45t+30t}{t}=75\)(km/h)
Vậy vận tốc của xe là 75(km/h)

ta có:
gọi t' là tổng thời gian đi trên nửa quãng đường cuối
vận tốc trung bình của người đó là:
\(v_{tb}=\frac{S_1+S_2+S_3}{t_1+t_2+t_3}=\frac{S}{t_1+t'}\) (*)
ta lại có:
thời gian đi trên nửa quãng đường đầu là:
\(t_1=\frac{S_1}{v_1}=\frac{S}{2v_1}=\frac{S}{60}\left(1\right)\)
tổng quãng đường lúc sau là:
\(S_2+S_3=\frac{S}{2}\)
\(\Leftrightarrow v_2t_2+v_3t_3=\frac{S}{2}\)
\(\Leftrightarrow25t_2+15t_3=\frac{S}{2}\)
\(\Leftrightarrow\frac{25t'+15t'}{2}=\frac{S}{2}\)
\(\Leftrightarrow40t'=S\Rightarrow t'=\frac{S}{40}\left(2\right)\)
lấy (1) và (2) thế vào phương trình (*) ta có:
\(v_{tb}=\frac{S}{\frac{S}{60}+\frac{S}{40}}=\frac{S}{S\left(\frac{1}{60}+\frac{1}{40}\right)}=\frac{1}{\frac{1}{60}+\frac{1}{40}}=24\)
vậy vận tốc trung bình của người này là 24km/h
trong 1/2 thời gian đầu người ấy đi được:
\(S''=\frac{t}{2}.v_{tb}=\frac{v_{tb}\left(t_1+t'\right)}{2}\)
\(\Leftrightarrow S''=\frac{24\left(\frac{S}{60}+\frac{S}{40}\right)}{2}\)
\(\Leftrightarrow S''=\frac{24\left(\frac{2S+3S}{120}\right)}{2}\)
\(\Leftrightarrow S''=\frac{\left(\frac{120S}{120}\right)}{2}\)
\(\Leftrightarrow S''=\frac{S}{2}\)
mình làm vậy bạn xem đúng ko nhé![]()
Gọi s là chiều dài nửa quãng đường mà người đi xe đạp phải đi.
Như vậy, thời gian đi hết nửa quãng đường đầu s1 = s với vận tốc v1 là:
Thời gian đi hết nửa quãng đường còn lại s2 = s với vận tốc v2 là:
Vậy tổng thời gian đi hết cả quãng đường là: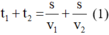
Vận tốc trung bình của người đi xe đạp trên cả quãng đường là: