Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án C
Áp dụng công thức: v v max 2 + a ω v max 2 = 1
⇒ 1 2 2 + − 10 3 2 ω 2 = 1 ⇒ ω = 10 rad/s
Vậy A = 20 cm
Tại t = 0 thì v = ± 1 ⇔ ± 1 = − 1 sin φ ⇒ φ = ± π 6 rad

Đáp án C
+ Áp dụng hệ thức độc lập thời gian với hai đại lượng vuông pha là vận tốc và gia tốc:


+ Từ phương trình v = 10 π c os 2 π t + 0 , 5 π = ω A cos 2 π t + φ + π 2
® x = 5 cos 2 π t .
® Quỹ đạo dao động là: L = 2 A = 10 cm
Tốc độ cực đại là v max = 10 π cm/s
Gia tốc cực đại là a max = ω 2 A = 20 π 2 c m / s 2
Tốc độ trung bình trong một chu kì là v t b = s T = 4 A T = 4.5 1 = 20 cm/s.
Tại t = 0 thì x = 5 ® vật ở vị trí biên.
® Các phát biểu đúng là: c, e.
Đáp án C

Đáp án C
+ Ta có: wA = 10π ® A = 5 cm
+ Phương trình của dao động là: x = 5cos(2πt) cm
+ Quỹ đạo dao động là: L = 2A = 10 cm
+ f = ω 2 π Hz => T = 1 s
+ amax = w2A = 20π2 cm/s2
+ vmax = wA = 10π cm/s
+ Trong 1 chu kì thì: v t b = s t = 4 A T = 20 cm/s
+ Khi t = 0 thì vật ở biên dương.
Vậy phát biểu đúng là (c) và (e).

+ Ta có: wA = 10π => A = 5 cm
+ Phương trình của dao động là: x = 5cos(2πt) cm
+ Quỹ đạo dao động là: L = 2A = 10 cm
+ f = ω 2 π = 1 Hz ® T = 1 s
+ amax = w2A = 20π2 cm/s2
+ vmax = wA = 10π cm/s
+ Trong 1 chu kì thì: v t b = s t = 4 A T = 20 cm/s
+ Khi t = 0 thì vật ở biên dương.
Vậy phát biểu đúng là (c) và (e).
ü Đáp án C

Chọn A
+ Thay (x1 = 3cm; v1 = 8π cm/s) và (x2 = 4cm; v2 = 6π cm/s) vào  ta được hệ phương trình hai ẩn A2 và
ta được hệ phương trình hai ẩn A2 và ![]()
. Giải hệ phương trình ta được A = 5cm và ω = 2π rad/s.
+ Tìm giá trị các đại lượng thay vào:
+ t = 0: vật qua vị trí cân bằng theo chiều dương => φ = - π/2 rad.
+ Thay số: x = 5cos(2πt - π/2)(cm).

Dùng công thức độc lập: \(A^2=x^2+\dfrac{v^2}{\omega^2}\)
Suy ra hệ:
\(A^2=3^2+\dfrac{(8\pi)^2}{\omega^2}\)
\(A^2=4^2+\dfrac{(6\pi)^2}{\omega^2}\)
Từ đó tìm được:
\(A=5cm\)
\(\omega=2\pi(rad/s)\)
Ban đầu, vật qua VTCB theo chiều âm, suy ra \(\varphi=\dfrac{\pi}{2}(rad)\)
Vậy PT dao động: \(x=5\cos(2\pi t+\dfrac{\pi}{2})cm\)
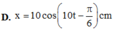

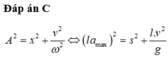
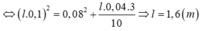
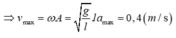
\(t=\dfrac{v-v_0}{a}\)
\(t=\dfrac{2\left(\dfrac{m}{s}\right)-1\left(\dfrac{m}{s}\right)}{-10\dfrac{m}{s^2}}=0,1\left(s\right)\)
Vậy thời gian để vật đi qua vị trí cân bằng là 0.1 giây.
\(x=x_0+v_0t+\dfrac{1}{2}at^2=0+1\left(\dfrac{m}{s}\right).0,1s+\dfrac{1}{2}.\left(-10\dfrac{m}{s^2}\right).\left(0,1s\right)^2=0,045m\)
Vậy phương trình dao động của vật là:
\(x=0,045-0,1t^2\)