Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nửa chu kỳ vật đi được quãng đường S=2A=10\(\Rightarrow A=5\left(cm\right)\)
Dùng công thức độc lập:
\(A^2=x^2+\frac{v^2}{\omega^2}\Leftrightarrow5^2=3^2+\frac{\left(16\pi\right)^2}{\omega^2}\Rightarrow\omega=4\pi\\ \Rightarrow T=\frac{1}{2}\left(s\right)\)
S=10 =>A=5
A2=x2 +v2/ω2 =>ω2=v2/(A2-x2) =>ω=4π
=>T=2π/ω=2π/4π=1/2=0,5s

Đáp án A
Biên độ dao động của vật: A 2 = x 2 + v 2 ω 2 = 5 2 + 25 2 5 2 = 50 ⇒ A = 5 2

Chọn A
+ Động năng và thế năng biến thiên với ω' = 2ω => T' = T/2
+ Thay (x1 = 4cm; v1 =40π√3 cm/s) và (x2 = 4√2 cm; v2 = 40π√2 cm/s) vào 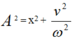 .ta được hệ phương trình hai ẩn A2 và
.ta được hệ phương trình hai ẩn A2 và ![]()
Giải hệ phương trình ta được ω = 10π rad/s => T = 0,2s => T' = 0,1 (s).

Chọn A
+ Thay (x1 = 3cm; v1 = 8π cm/s) và (x2 = 4cm; v2 = 6π cm/s) vào  ta được hệ phương trình hai ẩn A2 và
ta được hệ phương trình hai ẩn A2 và ![]()
. Giải hệ phương trình ta được A = 5cm và ω = 2π rad/s.
+ Tìm giá trị các đại lượng thay vào:
+ t = 0: vật qua vị trí cân bằng theo chiều dương => φ = - π/2 rad.
+ Thay số: x = 5cos(2πt - π/2)(cm).
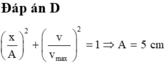
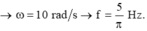
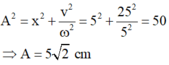

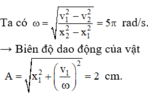

Dùng công thức độc lập
\(x^2+\frac{v^2}{\omega^2}=A^2\)
Ta có:
\(\begin{cases}3^2+\frac{\left(8\pi\right)^2}{\omega^2}=A^2\\4^2+\frac{\left(6\pi\right)^2}{\omega^2}=A^2\end{cases}\)\(\Leftrightarrow\begin{cases}A=5\\\omega=2\sqrt{10}\end{cases}\)
\(\Rightarrow T=\frac{2\pi}{\omega}=1\left(s\right)\\ 2s=2T\Leftrightarrow S=8A=40cm\)
à chị hay cô gì ơi. có thể ghi cái hệ đó ra để bấm máy được không ạ. Tại e bấm máy ra số lớn lắm ạ. Mong giúp đỡ