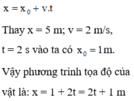Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình chuyển động thẳng đều có dạng tổng quát: \(x=x_0+v.t\)
+ \(t_1=2s\) suy ra: \(x_0+2v=6\) (1)
+ \(t_2=5s\) suy ra: \(x_0+5v=12\) (2)
Từ (1) và (2) suy ra hệ:
\(\left\{{}\begin{matrix}x_0+2v=6\\x_0+5v=12\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_0=2\\v=2\end{matrix}\right.\)
Vậy phương trình chuyển động là: \(x=2+2.t(m)\)

Giải:
a. Phương trình chuyển động và phương trình vận tốc

Vậy vật chuyển động chậm dần đều, để vật đổi chiều thì khi vật dừng lại nên
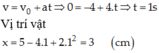

a. Phương trình chuyển động và phương trình vận tốc:
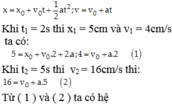

b. Ta có v 0 a < 0 vậy vật chuyển động chậm dần đều, để vật đổi chiều thì khi vật dừng lại nên
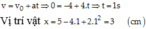

Giải:
Ta có phương trình chuyển động của vật x = x 0 + v t
Tại t 1 = 2 h thì x 1 = 8 m ⇒ 8 = x 0 + 2 v ( 1 )
Tại t 2 = 3 h thì x 2 = 12 m ⇒ 12 = x 0 + 3 v ( 2 )
Từ ( 1 ) và (2 ) ta có x 0 = 4 m ; v = 2 m / s
Vậy phương trình dao động là x = 4 + 2 t

Chọn đáp án D
? Lời giải:
+ Ta có phương trình chuyển động của vật