Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương pháp:
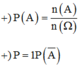
Cách giải: Số phần tử của không gian mẫu: ![]()
Gọi A: “Mỗi khối có ít nhất 1 học sinh được chọn.”
Khi đó ![]()
Xác suất: 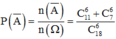
![]()
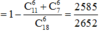

Đáp án C
TH1: 4 học sinh được chọn thuộc một lớp:
+ Lớp A có C 5 4 = 5 cách chọn.
+ Lớp B có C 4 4 = 1 cách chọn.
Trường hợp này có: 6 cách chọn.
TH2: 4 học sinh được chọn thuộc 2 lớp:
+ Lớp A và B: C 9 4 − C 5 4 + C 4 4 = 120 có .
+ Lớp B và C : C 7 4 − C 4 4 = 34 có
+ Lớp C và A: C 8 4 − C 5 4 = 65 có
Trường hợp này có 219 cách chọn.
Vậy có 225 cách chọn thỏa yêu cầu bài toán.

Đáp án B
Không gian mẫu n Ω = C 7 4
Gọi biến cố A: “Minh Anh được chọn trong 4 học sinh được chọn đi thi.”
+ Chọn Minh Anh đi thi có 1 cách.
+ Chọn 3 bạn trong 6 bạn còn lại có C 6 3 cách.
Suy ra n A = 1. C 6 3 = 20.
Vậy xác suất để Minh Anh được chọn đi thi là: P A = n A n Ω = 20 35 = 4 7 .

Số học sinh nam khối 6 chiếm 2/9 của 3/8 số học sinh nam toàn trường, nên số học sinh nam khối 6 chiếm: (2/9)*(3/8)= 1/12 số học sinh khá giỏi bộ môn toán toàn trường.
Số học sinh nữ khối 6 chiếm 4/9 của 5/8 số học sinh nứ toàn trường, nên số học sinh nữ khối 6 chiếm: (4/9)*(5/8) = 5/18 số học sinh khá giỏi bộ môn toán toàn trường
Tổng số học sinh nam và nữ khối 6 chiếm: 1/12 + 5/18 = 13/36 số học sinh khá giỏi bộ môn toán toàn trường
Vì số học sinh khá giỏi bộ môn toán toàn trường trong khoảng từ 70 đến 100 em và là 1 số chia hết cho 36 nên số học sinh khá giỏi bộ môn toán toàn trường là 72.
Số học sinh nam khá giỏi bộ môn toán là: (1/12)*72 = 6 học sinh
Số học sinh nữ khá giỏi bộ môn toán là: (5/18)*72 = 20 học sinh
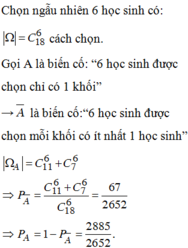
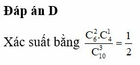



Chọn A
a nhé