Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

P |
| \(\overline P \) |
|
Dơi là một loài chim | Sai | Dơi không phải là một loài chim | Đúng |
\(\pi \) không phải là một số hữu tỉ | Đúng | \(\pi \) là một số hữu tỉ | Sai |
\(\sqrt 2 + \sqrt 3 > \sqrt 5 \) | Đúng | \(\sqrt 2 + \sqrt 3 \le \sqrt 5 \) | Sai |
\(\sqrt 2 .\sqrt {18} = 6\) | Đúng | \(\sqrt 2 .\sqrt {18} \ne 6\) | Sai |
Chú ý:
Hai mệnh đề cùng cặp luôn có một mệnh đề đúng và một mệnh đề sai.
Nếu P đúng thì \(\overline P \) sai và ngược lại.

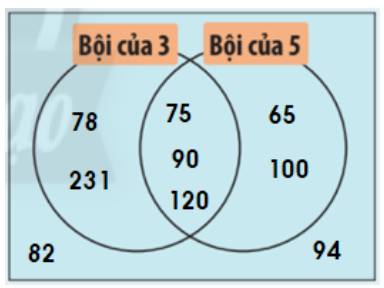
Bội của 3: 75, 78, 90, 120, 231
Bội của 5: 65, 75, 90, 100, 120
Vừa là bội của 3, vừa là bội của 5: 75, 90, 120.
Không là bội của 3 và không là bội của 5: 82, 94

a) Trong bảng phân bố trên, giá trị (tiền lương) 700 (nghìn đồng) và 900 (nghìn đồng) có cùng tần số bằng nhau và lớn hơn các tân số của các giá trị khác. Bảng phân bố này có hai số mốt là:
M1 = 700, M2 = 900.
b) Ý nghĩa: Tỉ lệ công nhân có mức lương 700 nghìn đồng và 900 nghìn đồng cao hơn tỉ lệ công nhân có các mức lương khác.i

![]() có thế mà cũng nhầm nhưng 1 điều mình mới học lớp 5 nên không thể trả lời câu hỏi của lớp 7
có thế mà cũng nhầm nhưng 1 điều mình mới học lớp 5 nên không thể trả lời câu hỏi của lớp 7
* Chú ý: Mk làm đại nên cx k bik đúng hay sai nx ![]()
Giải:
Ta có: \(\overline{X}\) = \(\frac{5.n+6.5+9.2+10.1}{n+5+2+1}\)
Thay: 6,8 = \(\frac{5.n+6.5+9.2+10.1}{n+5+2+1}\)
= \(\frac{5n+58}{n+8}\)
-> 6,8 (n+8) = 5n + 58
6,8 . 8 + 8n = 58 + 5n
54,4 + 8n = 5n + 58
=> 8n - 5n = 58 - 54,4
3n = 3,6
=>> n = 3,6 : 3
Vậy n = 1,2

a) Ta có x1 = 1 có tần số n1 = 2100 (lớn nhất)
=> Mốt của bảng phân bố đã cho là: Mo = 1
b) Trong sản xuất, nhà máy nên ưu tiên cho mẫu số 1

Từ bảng giá trị vận tốc v (mét/giây) ở thời điểm t (giây) của vật chuyển động, ta thấy ứng với mỗi thời điểm t (giây) trong bảng đều có một giá trị vận tốc v duy nhất. Vì vậy, bảng này biểu thị một hàm số.
Hàm số đó có tập xác định \(D = \{ 0,5;1;1,2;1,8;2,5\} \)