Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Giả sử bác An gửi số tiền tối thiểu hàng tháng là T (đồng). Đặt r = 0,45%.
Hết tháng thứ nhất bác An nhận được số tiền cả gốc và lãi là
T 1 = T + T . r = T . 1 + r .
Hết tháng thứ hai bác An nhận được số tiền cả gốc và lãi là
T 2 = T . 2 + r + T . 2 + r . r = T . r + 1 2 + r + 1 .
Bằng phương pháp quy nạp toán học, ta chứng minh được rằng sau n tháng gửi tiết kiệm thì bác An nhận được số tiền cả gốc và lãi là
T n = T 1 + r n + 1 + r n − 1 + ... + 1 + r .
Dễ dàng tính được T n = T r . 1 + r . 1 + r n − 1 .
Suy ra số tiền lãi sau n tháng gửi tiết kiệm là
L n = T n − T n = T r . 1 + r . 1 + r n − 1 − T n .
Theo giả thiết, ta có n = 36 , L 36 ≥ 30 000 000. Suy ra T ≥ 9 493 000.
Phân tích phương án nhiễu.
Phương án A: Sai do HS tính chỉ gửi 35 tháng.
Phương án B: Sai do HS sử dụng công thức của bài toán tính lãi kép và hiểu đề bài yêu cầu số tiền thu được sau 3 năm đủ để mua xe máy có trị giá 30 triệu đồng nên tìm được T = 25 523 000.
Phương án C: Sai do HS giải đúng như trên nhưng lại làm tròn T = 9 492 000.

Đây là bài toán lãi kép gửi một lần có công thức :
T=M.\(\left(r+1\right)^n\) trong đó :T:số tiền cả vốn lẫn lãi sau n kì hạn
M :số tiền gửi ban đầu
n:số kì hạn tính lãi
r:lãi suất định kì
như vậy ta có :
250 =100.\(\left(1+7\%\right)^n\)
\(\Leftrightarrow1,07^n\)=2,5 \(\Leftrightarrow\)n=\(\log\left(2,5\right)_{1,07}\) =13,54 vậy là đáp án B sau 13 năm

Ta có 2005 – 1985 = 20 (năm). Vậy đầu năm 2005 ứng với t = 20. Số cần tìm

Chọn đáp án A.
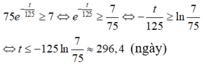


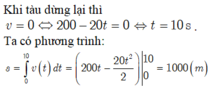
Con tàu hoạt động bình thường khi
Chọn đáp án B