Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi b, c là độ dài các cạnh góc vuông, a là độ dài cạnh huyền (tính bằng cm) ( 0 < b; c < a)
+) Do các cạnh góc vuông tỉ lệ với 7 và 24 nên:
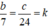 ⇒ b = 7k, c = 24k.
⇒ b = 7k, c = 24k.
Theo định lý Py-ta-go:
a2 = b2 + c2 = (7k)2 + (24k)2 = 625k2 = (25k)2
Nên a = 25k.
Theo đề bài, chu vi tam giác bằng 112 cm nên: a + b + c = 112 (cm).
Suy ra: 25k + 7k + 24k = 112
Hay 56k = 112
Từ đó ta tính được k = 2. Vậy a = 50cm.

Gọi chiều dài 2 cạnh góc vuông là a;b (a;b > 0) ; chiều dài cạnh huyền là c (c>0)
Với a > b
Ta có \(\frac{a}{24}=\frac{b}{7}\)
Đặt \(\frac{a}{24}=\frac{b}{7}=k\left(k>0\right)\Rightarrow\hept{\begin{cases}a=24k\\b=7k\end{cases}}\)
Vì tam giác đó vuông nên
a2 + b2 = c2 (định lý Py-ta-go)
=> (24k)2 + (7k)2 = c2
=> 576k2 + 49k2 = c2
=> 625k2 = c2
=> (25k)2 = c2
=> \(\orbr{\begin{cases}25k=c\left(tm\right)\\25k=-c\left(\text{loại vì }25k>0\text{ mà }-c< 0\right)\end{cases}}\)
=> 25k = c
Lại có a + b + c = 112
=> 24k + 7k + 25k = 112
=> 56k = 112
=> k = 2
=> c = 50
Vậy độ dài cạnh huyền là 50 cm

Gọi độ dài các cạnh góc vuông của tam giác lần lượt là 5k và 12k với k> 0. Dùng định lý Py-ta-go tính được độ dài cạnh huyền là 13k, do đó
5k +12k + 13k = 30 => k = 1.
Từ đó độ dài cạnh huyền là 13 cm.

Tìm được độ dài các cạnh của tam giác lần lượt là:
6 cm, 8 cm, 10 cm.

mk chỉ tính đc thôi ko bít cách làm
bài nỲ dùng ddingj lý pi-ta-go
nhưng mk chưa học đến
ko giúp đc bn

Gọi b, c là độ dài các cạnh góc vuông,a là độ dai cạnh huyền (tính bằng cm). Ta có:
\(\dfrac{b}{7}=\dfrac{c}{24}=k\Rightarrow b=7k,c=24k\)
Theo định lí Py-ta-go:
a2 = b2 + c2 = (7k)2 + (24k)2 = 625k2 = (25k)2
nên a = 25k
Theo đề bài a + b + c = 112 (cm). Từ đó ta tính được k = 2. Vậy a = 50cm.
Gọi b, c là độ dài các cạnh góc vuông,a là độ dai cạnh huyền (tính bằng cm). Ta có:
b7=c24=k⇒b=7k,c=24kb7=c24=k⇒b=7k,c=24k
Theo định lí Py-ta-go:
a2 = b2 + c2 = (7k)2 + (24k)2 = 625k2 = (25k)2
nên a = 25k
Theo đề bài a + b + c = 112 (cm). Từ đó ta tính được k = 2. Vậy a = 50cm.