Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi b, c là độ dài các cạnh góc vuông,a là độ dai cạnh huyền (tính bằng cm). Ta có:
\(\dfrac{b}{7}=\dfrac{c}{24}=k\Rightarrow b=7k,c=24k\)
Theo định lí Py-ta-go:
a2 = b2 + c2 = (7k)2 + (24k)2 = 625k2 = (25k)2
nên a = 25k
Theo đề bài a + b + c = 112 (cm). Từ đó ta tính được k = 2. Vậy a = 50cm.
Gọi b, c là độ dài các cạnh góc vuông,a là độ dai cạnh huyền (tính bằng cm). Ta có:
b7=c24=k⇒b=7k,c=24kb7=c24=k⇒b=7k,c=24k
Theo định lí Py-ta-go:
a2 = b2 + c2 = (7k)2 + (24k)2 = 625k2 = (25k)2
nên a = 25k
Theo đề bài a + b + c = 112 (cm). Từ đó ta tính được k = 2. Vậy a = 50cm.

Gọi b, c là độ dài các cạnh góc vuông, a là độ dài cạnh huyền (tính bằng cm) ( 0 < b; c < a)
+) Do các cạnh góc vuông tỉ lệ với 7 và 24 nên:
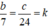 ⇒ b = 7k, c = 24k.
⇒ b = 7k, c = 24k.
Theo định lý Py-ta-go:
a2 = b2 + c2 = (7k)2 + (24k)2 = 625k2 = (25k)2
Nên a = 25k.
Theo đề bài, chu vi tam giác bằng 112 cm nên: a + b + c = 112 (cm).
Suy ra: 25k + 7k + 24k = 112
Hay 56k = 112
Từ đó ta tính được k = 2. Vậy a = 50cm.

Gọi a,b,c lần lượt là 2 cạnh góc vuông và cạnh huyền của tam giác đó
Theo đề ta có: \(\dfrac{a}{5}=\dfrac{b}{12}\)
Đặt: \(\dfrac{a}{5}=\dfrac{b}{12}=k\)
\(\Rightarrow\left\{{}\begin{matrix}a=5k\\b=12k\end{matrix}\right.\)
Tam giác đó vuông. Áp dụng Pitago
=> a2 + b2 = c2
\(\Rightarrow25k^2+144k^2=c^2\)
\(\Rightarrow c^2=169k^2\)
=> c = 13k
Chu vi của tam giác đó = 30
=> a + b + c = 30
=> 5k + 12k + 13k = 30
=> 30k = 30
=> k = 1
c = 13k = 13.1 = 13 (cm)
Vậy độ dài cạnh huyền là 13cm

Gọi độ dài các cạnh góc vuông của tam giác lần lượt là 5k và 12k với k> 0. Dùng định lý Py-ta-go tính được độ dài cạnh huyền là 13k, do đó
5k +12k + 13k = 30 => k = 1.
Từ đó độ dài cạnh huyền là 13 cm.

Gọi chiều dài 2 cạnh góc vuông là a;b (a;b > 0) ; chiều dài cạnh huyền là c (c>0)
Với a > b
Ta có \(\frac{a}{24}=\frac{b}{7}\)
Đặt \(\frac{a}{24}=\frac{b}{7}=k\left(k>0\right)\Rightarrow\hept{\begin{cases}a=24k\\b=7k\end{cases}}\)
Vì tam giác đó vuông nên
a2 + b2 = c2 (định lý Py-ta-go)
=> (24k)2 + (7k)2 = c2
=> 576k2 + 49k2 = c2
=> 625k2 = c2
=> (25k)2 = c2
=> \(\orbr{\begin{cases}25k=c\left(tm\right)\\25k=-c\left(\text{loại vì }25k>0\text{ mà }-c< 0\right)\end{cases}}\)
=> 25k = c
Lại có a + b + c = 112
=> 24k + 7k + 25k = 112
=> 56k = 112
=> k = 2
=> c = 50
Vậy độ dài cạnh huyền là 50 cm
chu vi tam giai bai nay mk chiu han
mk chỉ tính đc thôi ko bít cách làm
bài nỲ dùng ddingj lý pi-ta-go
nhưng mk chưa học đến
ko giúp đc bn