Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

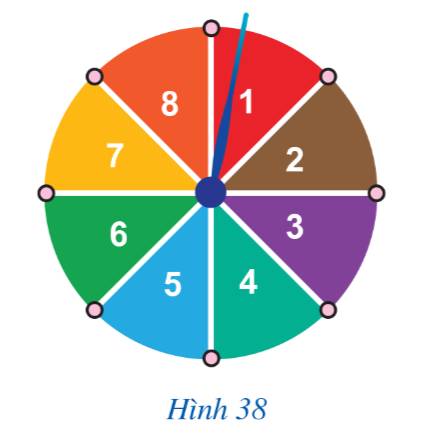
Khi quay tấm bìa, các kết quả có thể xảy ra là:
Mũi tên chỉ vào ô số 1; Mũi tên chỉ vào ô số 2; Mũi tên chỉ vào ô số 3; Mũi tên chỉ vào ô số 4; Mũi tên chỉ vào ô số 5; Mũi tên chỉ vào ô số 6; Mũi tên chỉ vào ô số 7; Mũi tên chỉ vào ô số 8.
- Các kết quả thuận lợi cho biến cố \(A\) mũi tên chỉ vào ô số chẵn là ô số 2; ô số 4; ô số 6; ô số 8.
- Các kết quả thuận lợi cho biến cố \(B\)mũi tên chỉ vào ô số chia hết cho 4 là ô số 4; ô số 8.
- Các kết quả thuận lợi cho biến cố \(C\) mũi tên chỉ vào ô số nhỏ hơn 3 là ô số 1; ô số 2.

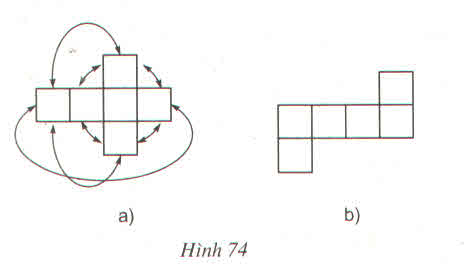
Mỗi hình vuông tương ứng với một mặt của hình lập phương có 6 mặt. Đầu tiên chúng ta giữ cố định một hình vuông ở giữa để làm một mặt trong cùng của hình lập phương, sau đó di chuyển các hình vuông còn lại theo chiều mũi tên như sau để được hình lập phương:

Số kết quả có thể xảy ra là: 8
Tập hợp các kết quả thuận lợi của biến cố “Mũi tên chỉ vào hình quạt ghi số nhỏ hơn 6” là:
\(A = \left\{ {1;2;3;4;5} \right\}\)
Số kết quả thuận lợi là 5
Vì thế, xác suất của biến cố đó là: \(\frac{5}{8}\)

Có 15 quả bóng màu xanh, 13 quả bóng màu đỏ và 17 quả bóng màu trắng => Có 45 kết quả có thể. Các kết quả có thể này là đồng khả năng
a) Có 15 quả bóng màu xanh => Có 15 kết quả thuận lợi cho biến cố C
Vậy \(P(C) = \frac{{15}}{{45}} = \frac{1}{3}\)
b) Có 13 quả bóng màu đỏ => Có 13 kết quả thuận lợi cho biến cố D
Vậy \(P(D) = \frac{{13}}{{45}}\)
c) Có 28 kết quả thuận lợi cho biến cố E
Vậy \(P(E) = \frac{{28}}{{45}}\)

Đáp án đúng là C
Số lần lấy được thẻ màu đỏ là \(50 - 14 = 36\) (lần)
Xác suất thực nghiệm của biến cố “Lấy được thẻ màu đỏ” là \(\frac{{36}}{{50}} = 0,72\)

Mỗi hình vuông tương ứng với một mặt của hình lập phương có 6 mặt. Đầu tiên chúng ta giữ cố định một hình vuông ở giữa để làm một mặt trong cùng của hình lập phương, sau đó di chuyển các hình vuông còn lại theo chiều mũi tên như sau để được hình lập phương:


Có 20 kết quả có thể, đó là 1; 2;...; 20. Do 20 hình quạt như nhau nên 20 kết quả có thể này là đồng khả năng
a) Có 4; 8; 12; 16; 20 chia hết cho 4 => Có 5 hình quạt ghi số chia hết cho 4
Vậy xác suất để mũi tên chỉ vào hình quạt ghi số chia hết cho 4 là: \(\frac{4}{{20}} = \frac{1}{5}\)
b) Có số 1; 4; 6; 8; 9; 10; 12; 14; 15; 16; 18; 20 không phải số nguyên tố => Có 12 hình quạt ghi số không phải là số nguyên tố
Vậy xác suất để mũi tên chỉ vào hình quạt ghi số không phải là số nguyên tố là: \(\frac{12}{{20}} = \frac{3}{5}\)

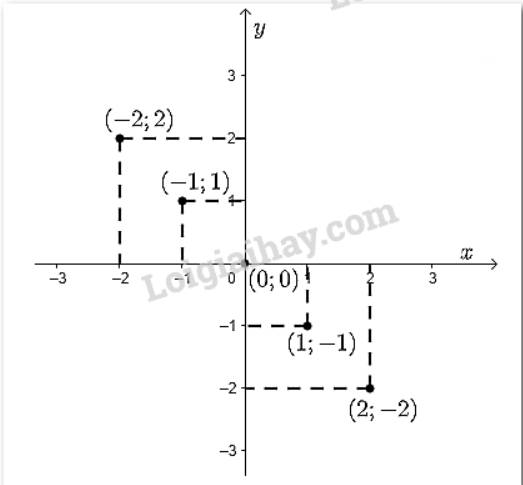
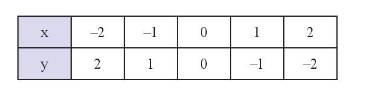
Đồ thị hàm số là tập hợp các điểm có tọa độ \(\left( { - 2;2} \right);\left( { - 1;1} \right);\left( {0;0} \right);\left( {1; - 1} \right);\left( {2; - 2} \right)\) được vẽ trên mặt phẳng tọa độ như hình dưới đây:
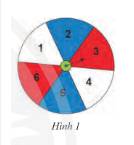
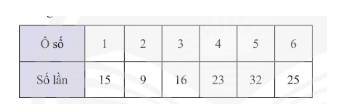


a) Ô màu trắng được đánh số 1 và số 4 nên số lần mũi tên chỉ vào ô màu trắng là:
\(15 + 23 = 38\) (lần)
Xác suất thực nghiệm của biến cố mũi tên chỉ vào ô có màu trắng là \(\frac{{38}}{{120}} = \frac{{19}}{{60}}\).
b) Dự đoán xác suất thực nghiệm mũi tên chỉ vào mỗi ô là không như nhau.
c) Ô màu đỏ được đánh số 3 và số 6 nên số lần mũi tên chỉ vào ô màu đỏ là:
\(16 + 25 = 41\) (lần)
Xác suất thực nghiệm của biến cố mũi tên chỉ vào ô có màu đỏ là \(\frac{{41}}{{120}}\).
Ô màu xanh được đánh số 2 và số 5 nên số lần mũi tên chỉ vào ô màu xanh là:
\(9 + 32 = 41\) (lần)
Xác suất thực nghiệm của biến cố mũi tên chỉ vào ô có màu xanh là \(\frac{{41}}{{120}}\).
Vì thực nghiệm của biến cố mũi tên chỉ vào ô màu trắng khác xác suất thực nghiệm mũi tên chỉ vào ô màu đỏ và xác suất thực nghiệm mũi tên chỉ vào ô màu xanh \(\left( {\frac{{41}}{{120}} \ne \frac{{19}}{{60}}} \right)\).
Do đó, kết quả thực nghiệm của bạn Thủy là chưa phù hợp với nhận định.