Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(m=2kg;m_1=0,5kg\Rightarrow m_2=2-0,5=1,5kg\)
Động lượng vật thứ nhất:
\(p_1=m_1\cdot v_1=0,5\cdot400=200kg.m\)/s
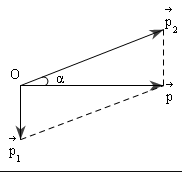
Bảo toàn động lượng: \(\overrightarrow{p_1}+\overrightarrow{p_2}=\overrightarrow{p}\)
\(\Rightarrow200+1,5\cdot v_2=2\cdot200\Rightarrow v_2=\dfrac{400}{3}\approx133,33\)m/s
Viên đạn bay theo hướng:
\(cos\alpha=\dfrac{p}{p_2}=\dfrac{2\cdot200}{1,5\cdot\dfrac{400}{3}}=2\)
\(\Rightarrow\alpha=arctan2\)

Khi đạn nổ bỏ qua sức cản của không khí nên được coi như là một hệ kín. Vận tốc mảnh nhỏ trước khi nổ là
v 1 / 2 − v 1 2 = 2 g h ⇒ v 1 = v 1 / 2 − 2 g h ⇒ v 1 = 100 2 − 2.10.125 = 50 3 ( m / s )
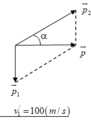
Theo định luật bảo toàn động lượng
p → = p → 1 + p → 2
Với
p = m v = ( 2 + 3 ) .50 = 250 ( k g m / s ) p 1 = m 1 v 1 = 2.50 3 = 100 3 ( k g m / s ) p 2 = m 2 v 2 = 3. v 2 ( k g m / s )
Vì v → 1 ⊥ v → ⇒ p → 1 ⊥ p → theo pitago
⇒ p 2 2 = p 1 2 + P 2 ⇒ p 2 = p 1 2 + p 2 = ( 100 3 ) 2 + 250 2 = 50 37 ( k g m / s )
⇒ v 2 = p 2 3 = 50 37 3 ≈ 101 , 4 ( m / s )
Mà sin α = p 1 p 2 = 100 3 50 37 ⇒ α = 34 , 72 0

Khi đạn nổ bỏ qua sức cản của không khí nên được coi như là một hệ kín.
Vận tốc mảnh nhỏ trước khi nổ là:
v 1 / 2 = v 1 2 = 2 g h ⇒ v 1 = v 1 / 2 − 2 g h
⇒ v 1 = 100 2 − 2.10.125 = 50 3 m / s
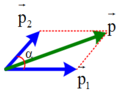
+ Theo định luật bảo toàn động lượng: p → = p → 1 + p → 2
Với p = m v = 2 + 3 .50 = 250 k g . m / s
p 1 = m 1 v 1 = 2.50 3 = 100 3 k g . m / s p 2 = m 2 . v 2 = 3. v 2 k g . m / s
+ Vì v → 1 ⊥ v → 2 ⇒ p → 1 ⊥ p → Theo pitago
p 2 2 = p 1 2 + p 2 ⇒ p 2 = p 1 2 + p 2 = 100 3 2 + 250 2 = 50 37 k g . m / s
⇒ v 2 = p 2 3 = 50 37 3 ≈ 101 , 4 m / s + sin α = p 1 p 2 = 100 3 50 37 ⇒ α = 34 , 72 0
Chọn đáp án B

Xe tiếp tục chuyển động theo chiều cũ với vận tốc 0,3m/s. Vì ngoại lực tác dụng lên hệ là trọng lực, rất nhỏ so với nội lực tương tác (lực làm vỡ viên đạn thành hai mảnh) nên động lượng của hệ ngay trước và sau khi đạn vỡ được bảo toàn.
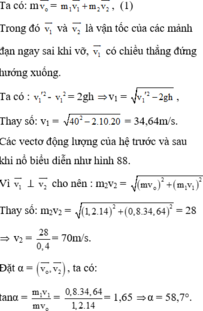
Vậy, ngay sau khi vỡ, mảnh đạn thứ hai bay chếch lên, nghiêng góc 58,7° so với phương ngang với vận tốc 70m/s.
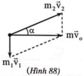

Ta có : m . v0 = m1v1 + m2v2
Trong đó v1 v2 là vận tốc các nửa mảnh đạn ngay sau khi vỡ, v1 có chiều thẳng đứng
Ta có : \(v^2_1-v^2_1=2gh\)
\(\Rightarrow v_1=\sqrt{v_1^2-2gh}=\sqrt{40^2-20.10.20}=20\sqrt{3}\) (m/s)
Vì v0 vuông góc với v1
Nên m2 . v2 = \(\sqrt{\left(mv_0\right)^2+\left(m_1v_1\right)^2}\)
\(m_2v_2=\sqrt{\left(0,8.12,5\right)^2+\left(0,5.20\sqrt{3}\right)^2}=20\)
\(m_2v_2=20kg\) (m/s)
\(v_2=\frac{20}{m^2}=\frac{20}{0,3}\approx66,7m\)
Đặt a v0 , v2 Ta có tga = \(\frac{m_1v_1}{mv_0}=\sqrt{3}\Rightarrow a=60^o\)
Vậy ngay sau khi nổ, mảnh đạn II bay chếch lên, nghiêng góc α = 60o so với phương ngang với vận tốc 66,7 m/s.

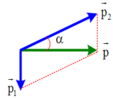
Khi đạn nổ bỏ qua sức cản của không khí nên được coi như là một hệ kín.
Vận tốc của mảnh nhỏ trước khi nổ là:
v 1 / − v 1 2 = 2 g h ⇒ v 1 = v 1 / 2 − 2 g h
Theo định luật bảo toàn động lượng: p → = p → 1 + p → 2
+ Với p = m v = 0 , 5 + 0 , 3 .12 , 5 = 10 k g . m / s p 1 = m 1 v 1 = 0 , 5.20 3 = 10 3 k g . m / s p 2 = m 2 v 2 = 0 , 3 v 2 k g . m / s
+ Vì v → 1 ⊥ v → 2 ⇒ p → 1 ⊥ p → theo pitago
⇒ p 2 2 = p 1 2 + p 2 ⇒ p 2 = p 1 2 + p 2 = 10 3 2 + 10 2 = 20 k g m / s
⇒ v 2 = p 2 0 , 3 = 20 0 , 3 ≈ 66 , 7 m / s
+ Mà sin α = p 1 p 2 = 10 3 20 ⇒ α = 60 0
Vậy mảnh hai chuyển động theo phương hợp với phương thẳng đứng một góc 60° với vận tốc 66,67 (m/s)
Chọn đáp án B

Khi đạn nổ bỏ qua sức cản của không khí nên được coi như là một hệ kín. Vận tốc mảnh nhỏ trước khi nổ là
v 1 / 2 − v 1 2 = 2 g h ⇒ v 1 = v 1 / 2 − 2 g h ⇒ v 1 = 40 2 − 2.10.20 = 20 3 ( m / s )
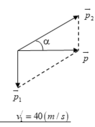
Theo định luật bảo toàn động lượng p → = p → 1 + p → 2
Với p = m v = ( 0 , 5 + 0 , 3 ) .12 , 5 = 10 ( k g m / s ) p 1 = m 1 v 1 = 0 , 5.20 3 = 10 3 ( k g m / s ) p 2 = m 2 v 2 = 0 , 3. v 2 ( k g m / s )
Vì v → 1 ⊥ v → ⇒ p → 1 ⊥ p → t h e o p i t a g o ⇒ p 2 2 = p 1 2 + P 2 ⇒ p 2 = p 1 2 + p 2 = ( 10 3 ) 2 + 10 2 = 20 ( k g m / s )
⇒ v 2 = p 2 0 , 3 = 20 0 , 3 ≈ 66 , 67 ( m / s ) M à sin α = p 1 p 2 = 10 3 20 ⇒ α = 60 0
Vậy mảnh hai chuyển động theo phương hợp với phương ngang một góc 60 0 với vận tốc 66 , 67 ( m / s )

Câu 1.
Bảo toàn động lượng: \(\overrightarrow{p_1}+\overrightarrow{p_2}=\overrightarrow{p}\)
\(\Rightarrow m_1v_1+m_2v_2=\left(m_1+m_2\right)V\)
Mà \(m_2=2m_1\)
\(\Rightarrow m_1\cdot200+2m_1\cdot v_2=\left(m_1+2m_1\right)\cdot100\)
\(\Rightarrow200+2v_2=300\)
\(\Rightarrow v_2=50\)m/s
Câu 2.
Cơ năng hệ tại A:
\(W_A=W_đ+W_t=\dfrac{1}{2}mv^2+mgz=\dfrac{1}{2}\cdot m\cdot0^2+m\cdot10\cdot24=240m\left(J\right)\)Cơ năng tại B:
\(W_B=W_đ+W_t\)
Mà \(W_t=\dfrac{1}{3}W_đ\Rightarrow W_đ=3W_t\)
\(\Rightarrow W_B=3W_t+W_t=4W_t=4mgh\)
Bảo toàn cơ năng: \(W_A=W_B\)
\(\Rightarrow240m=4mgh\)
\(\Rightarrow h=\dfrac{240}{4g}=\dfrac{240}{4\cdot10}=6m\)

Bài 1 :
P1 =m1g => m1 = 1(kg)
P2 = m2g => m2 =1,5(kg)
Trước khi nổ, hai mảnh của quả lựu đạn đều chuyển động với vận tốc v0, nên hệ vật có tổng động lượng : \(p_0=\left(m_1+m_2\right)v_0\)
Theo đl bảo toàn động lượng : \(p=p_0\Leftrightarrow m_1v_1+m_2v_2=\left(m_1+m_2\right)v_0\)
=> \(v_1=\frac{\left(m_1+m_2\right)v_0-m_2v_2}{m_1}=\frac{\left(1+1,5\right).10-1,5.25}{1}=-12,5\left(m/s\right)\)
=> vận tốc v1 của mảnh nhỏ ngược hướng với vận tốc ban đầu v0 của quả lựu đạn.
Bài2;
Vận tốc mảnh nhỏ trước khi nổ là :
v02=\(v_1^2=2gh\)
=> v1 = \(\sqrt{v_0^2-2gh}=\sqrt{100^2-2.10.125}=50\sqrt{3}\left(m/s\right)\)
Theo định luật bảo toàn động lượng :
\(\overrightarrow{p}=\overrightarrow{p_1}+\overrightarrow{p_2}\)
p = mv = 5.50 =250(kg.m/s)
\(\left\{{}\begin{matrix}p_1=m_1v_1=2.50\sqrt{3}=100\sqrt{3}\left(kg.m/s\right)\\p_2=m_2v_2=3.v_2\left(kg.m/s\right)\end{matrix}\right.\)
+ Vì \(\overrightarrow{v_1}\perp\overrightarrow{v_2}\rightarrow\overrightarrow{p_1}\perp\overrightarrow{p_2}\)
=> p2 = \(\sqrt{p_1^2+p^2}=\sqrt{\left(100\sqrt{3}\right)^2+250^2}=50\sqrt{37}\left(kg.m/s\right)\)
=> v2= \(\frac{p_2}{m_2}=\frac{50\sqrt{37}}{3}\approx101,4m/s+sin\alpha=\frac{p_1}{p_2}=\frac{100\sqrt{3}}{50\sqrt{3}}\)
=> \(\alpha=34,72^o\)
346(m/s)346(m/s)
Giải thích các bước giải:
p=mv=400(kg.m/s)p1=m1v1=200(kg.m/s)→p=→p1+→p2⇒p2=√p2+p21−2pp1cos600=200√3=346(kg.m/s)⇒m2v2=346⇒v2=346(m/s