Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi vận tốc dự định là \(x\left(km/h\right)x>6\)
Thực tế \(\left(x-6\right),\left(x+12\right)\)
Thời gian dự định \(t=\frac{80}{x}\)
Thời gian thực tế \(\frac{40}{\left(x-6\right)}+\frac{40}{\left(x+12\right)}\)
Ta có pt: \(\frac{80}{x}=\frac{40}{\left(x-6\right)}+\frac{40}{\left(x+12\right)}\)
\(\Leftrightarrow x=24\)
Vận tốc dự định là \(24km/h\)

Gọi x(km/h) là vận tốc dự định của ô tô đi từ A đến B
y(h) là thời gian dự định của ô tô đi từ A đến B
đk: x>10 , y>1
xy(km) là quãng đường từ A đến B
Nếu vận tốc tăng 20 km/h thì thời gian giảm 1h nên ta có phương trình:
xy=(x+20)(y-1) (1)
Nếu vận tốc giảm 10km/h thì thời gian tăng 1h nên ta có phương trình:
xy=(x-10)(y+1) (2)
Từ (1) và (2) ta có hệ phương trình:
{xy=(x+20)(y−1)xy=(x−10)(y+1)⇔{xy=xy−x+20y−20xy=xy+x−10y−10{xy=(x+20)(y−1)xy=(x−10)(y+1)⇔{xy=xy−x+20y−20xy=xy+x−10y−10
⇔{x−20y=−20−x+10y=−10⇔{−10y=−30−x=10y=−10⇔{x−20y=−20−x+10y=−10⇔{−10y=−30−x=10y=−10
y=3\\-x+10.3=-10
\Vậy vận tốc dự định của ô tô là 40km/h; thời gian dự định của ô tô là 3h

Gọi vận tốc ô tô dự định là v (km/h), (v > 6)
Thời gian đi nửa quãng đường đầu là 30/(v+10) (h)
Thời gian đi nửa quãng đường sau là 30/(v-6) (h)
Thời gian dự định đi quãng đường AB là 60/v (h)
Theo bài ra ta có:
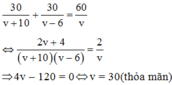
Vậy thời gian dự định là 60/30 = 2 giờ
Đáp án: B
Lời giải:
Giả sử vận tốc dự định là $a$ km/h. ĐK: $a>6$
Thời gian dự định: $\frac{60}{a}$.
Thời gian ô tô đi nửa quãng đường đầu: $\frac{30}{a-6}$ (h)
Thời gian ô tô đi nửa quãng đường sau: $\frac{30}{a+10}$ (h)
Vì ô tô vẫn đảm bảo thời gian dự định nên:
$\frac{30}{a-6}+\frac{30}{a+10}=\frac{60}{a}$
Với điều kiện $a>6$ ta dễ dàng giải ra $a=30$ (km/h)
Thời gian dự định là: $\frac{60}{a}=\frac{60}{30}=2$ (h)