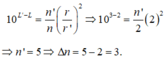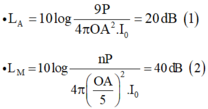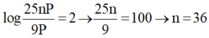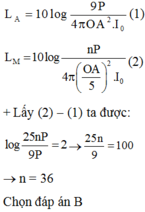Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Công thức chung cho điểm M cách nguồn O 1 đoạn MO: I M = P 4 π M O 2 = I 0 .10 L M
Áp dụng công thức với:
+ Điểm A: khi có 1 nguồn âm: P 4 π A O 2 = I 0 .10 3
+ Điểm B: khi có 1 nguồn âm: P 4 π B O 2 = I 0 .10 L B
+ Điểm H: (chân đường vuông góc kẻ từ O đến AB) đây là điểm có mức cường độ âm lớn nhất vì gần nguồn nhất. Có 64 P 4 π H O 2 = I 0 .10 5
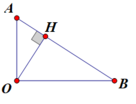
Có tam giác OAB vuông tại O, OH vuông góc AB
=> 1 O H 2 = 1 O A 2 + 1 O B 2 ⇒ 10 3 + 10 L B = 10 5 64 ⇒ L B = 2 , 75 ( B )

Đáp án B
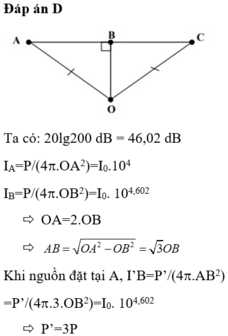
Mức cường độ âm tại A,B bằng nhau nên OA = OB . Mức cường độ âm tại C cực đại nên C là trung điểm của AB


Đáp án B
Vì mức cường độ âm tại A và B bằng nhau nên suy ra OA = OB. C có mức cđ âm max nên C gần O nhất, hay OC vuông góc với AB.
Có P 4 π O A 2 = I 0 .10 L P 4 π O C 2 = I 0 .10 L m ax ⇒ 10 L max − L = O A O C 2 ⇒ 10 0 , 3 = O A O C 2 ⇒ O C = 2 , 1238 ( m )
⇒ A B = 2 A C = 2 O A 2 − O C 2 ≈ 4 , 2376 ( m ) ⇒ t = A B v = 3 , 5313 ( s )

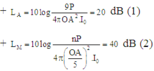
+ Lấy (2) - (1) ta được: log 25 n P 9 P = 2 → 25 n 9 = 100 → n = 36
Đáp án B