Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x là diện tích trồng đậu, y là diện tích trồng cà, (đơn vị a = 100 m 2 ), điều kiện x ≥ 0, y ≥ 0, ta có x + y ≤ 0
Số công cần dùng là 20x + 30y ≤ 180 hay 20 + 3y ≤ 18
Số tiền thu được là
F = 3000000x + 4000000y (đồng)
Hay F = 3x + 4y (đồng)
Ta cần tìm x, y thỏa mãn hệ bất phương trình
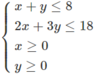
Sao cho F = 3x + 4y đạt giá trị lớn nhất.
Biểu diễn tập nghiệm của (H) ta được miền tứ giác OABC với A(0;6), B(6;2), C(8;0) và O(0;0).
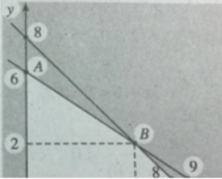
Xét giá trị của F tại các đỉnh O, A, B, C và so sánh ta suy ra x = 6, y = 2 (tọa độ điểm B) là diện tích cần trồng mỗi loại để thu được nhiều tiền nhất là F = 26 (triệu đồng).
Đáp số: Trồng 6a đậu, 2a cà, thu hoạch 26 000 000 đồng.

Tham khảo:
Gọi x, y lần lượt là số hũ tương cà loại A, loại B mà chủ nông trại cần làm.
Ta có các điều kiện ràng buộc đối với x, y như sau:
- Hiển nhiên \(x \ge 0,y \ge 0\)
- Có 180 kg cà chua nên \(10x + 5y \le 180\)
- Có 15 kg hành tây nên \(x + 0,25y \le 15\)
- Số hũ tương loại A ít nhất gấp 3,5 lần số hũ tương loại B nên \(x \ge 3,5y\)
Từ đó ta có hệ bất phương trình:
\(\left\{ \begin{array}{l}10x + 5y \le 180\\x + 0,25y \le 15\\x \ge 3,5y\\x \ge 0\\y \ge 0\end{array} \right.\)
Biểu diễn từng miền nghiệm của mỗi bất phương trình trên hệ trục tọa độ Oxy.

Miền không gạch chéo (miền tam giác OAB, bao gồm cả các cạnh) trong hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phương trình đã cho.
Với các đỉnh \(O(0;0),A(14;4),\)\(B(15;0).\)
Gọi F là số tiền lãi (đơn vị: nghìn đồng) thu được, ta có: \(F = 200x + 150y\)
Tính giá trị của F tại các đỉnh của tứ giác:
Tại \(O(0;0),\)\(F = 200.0 + 150.0 = 0\)
Tại \(A(14;4),\)\(F = 200.14 + 150.4 = 3400\)
Tại \(B(15;0),\)\(F = 200.15 + 150.0 = 3000\)
F đạt giá trị lớn nhất bằng \(3400\) nghìn đồng tại \(A(14;4).\)
Vậy chủ nông trại đó nên làm 14 hũ loại A và 4 hũ loại B để tiền lãi thu được là lớn nhất.

Diện tích khu đất hình vuông có trồng chè và cà phê là:
3x3=9(km2)
Diện tích trồng chè là:
9:(2+1)x1=3(km2)
Diện tích trồng cà phê là:
9 - 3 = 6 (km2)
Đáp số: 3 (km2)
diện tích khu đất hunhf chữ nhật là:
3.3=9(km2)
diện tích trồng chè là:
9:(2+1)=3(km2)
diện tích trồng cà phê là:
9-3=6(km2)
Đáp số: diện tích trồng chè là 3km2
diện tích trồng cà phê là 6km2
a)
Để quy hoạch x sào đất trồng cà tím, cần \(200\,000.x\)(đồng)
Để quy hoạch y sào đất trồng cà chua, cần \(100\,000.y\)(đồng)
Tổng số tiền để mua hạt giống là \(200{\rm{ }}000.x + 100{\rm{ }}000.y\) (đồng), tối đa là 9 triệu đồng nên ta có bất phương trình: \(0,2x + 0,1y \le 9\)
Ngoài ra số sào đất là số không âm nên \(x \ge 0\) và \(y \ge 0\)
b) + Cặp số (20; 40) thỏa mãn cả 3 bất phương trình trên vì \(0,2.20 + 0,1.40 = 8 < 9\).
+ Cặp số (40; 20) không thỏa mãn các bất phương trình trên vì \(0,2.40 + 0,1.20 = 10 > 9\).
+ Cặp số (-30; 10) không thỏa mãn các bất phương trình trên vì \( - 30 < 0\).