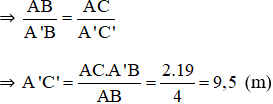Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

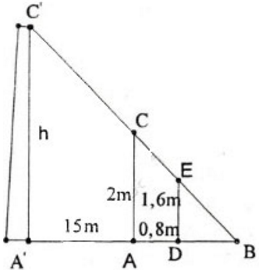
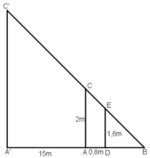
Gọi chiều cao của cây là h = A'C' và cọc tiêu AC = 2m.
Khoảng cách từ chân đến mắt người đo là DE = 1,6m.
Cọc xa cây một khoảng A'A = 15m, và người cách cọc một khoảng AD = 0,8m và gọi B là giao điểm của C'E và A'A.
Ta có: A’C’ ⊥ A’B, AC ⊥ A’B, DE ⊥ A’B
⇒ A’C’ // AC // DE.
Ta có: ΔDEB  ΔACB (vì DE // AC)
ΔACB (vì DE // AC)

Mà AB – DB = AD = 0,8
⇒ BD = 0,8.4 =3,2m; AB = 5.0,8 = 4m.
⇒ A'B = A'A + AD + DB = 15 + 0,8 + 3,2 = 19m
+ ΔACB  ΔA’C’B (vì AC // A’C’)
ΔA’C’B (vì AC // A’C’)
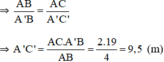
Vậy cây cao 9,5m.

Gọi chiều cao của cây là h = A'C' và cọc tiêu AC = 2m.
Khoảng cách từ chân đến mắt người đo là DE = 1,6m.
Cọc xa cây một khoảng A'A = 15m, và người cách cọc một khoảng AD = 0,8m và gọi B là giao điểm của C'E và A'A.
Ta có: A’C’ ⊥ A’B, AC ⊥ A’B, DE ⊥ A’B
⇒ A’C’ // AC // DE.
Ta có: ΔDEB 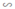 ΔACB (vì DE // AC)
ΔACB (vì DE // AC)

Mà AB – DB = AD = 0,8
⇒ BD = 0,8.4 =3,2m; AB = 5.0,8 = 4m.
⇒ A'B = A'A + AD + DB = 15 + 0,8 + 3,2 = 19m
+ ΔACB 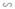 ΔA’C’B (vì AC // A’C’)
ΔA’C’B (vì AC // A’C’)
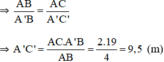
Vậy cây cao 9,5m.

Lời giải
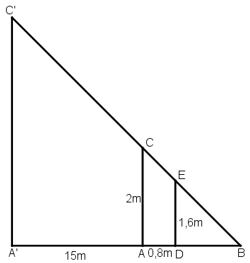
Gọi chiều cao của cây là h = A'C' và chọn một cọc tiêu AC = 2m.
Khoảng cách từ chân đến mắt người đo là DE = 1,6m.
Cọc xa cây một khoảng A'A = 15m, và người cách cọc một khoảng AD = 0,8m và gọi B là giao điểm của C'E và A'A.
Giải:
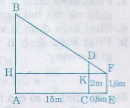
Giả sử AB là cây cần do, CD là cọc EF là khoảng cách từ mắt tới chân.
∆KDF ∽ ∆HBF
=> HBKD=HFKFHBKD=HFKF
=> HB = HF.KDKFHF.KDKF
mà HF = HK + KF =AC + CE = 15 + 0,8 = 15.8m
KD = CD - CK = CD - EF = 2 - 1,6 = 0,4 m
Do đó: HB = 7,9 m
Vậy chiều cao của cây là 7,9 m.

Gọi chiều cao của cây là h = A'C' và cọc tiêu AC = 2m.
Khoảng cách từ chân đến mắt người đo là DE = 1,6m.
Cọc xa cây một khoảng A'A = 15m, và người cách cọc một khoảng AD = 0,8m và gọi B là giao điểm của C'E và A'A.
Ta có: A’C’ ⊥ A’B, AC ⊥ A’B, DE ⊥ A’B
⇒ A’C’ // AC // DE.
Ta có: ΔDEB 
Mà AB – DB = AD = 0,8
⇒ BD = 0,8.4 =3,2m; AB = 5.0,8 = 4m.
⇒ A'B = A'A + AD + DB = 15 + 0,8 + 3,2 = 19m
+ ΔACB 
Vậy cây cao 9,5m.

C' A' A D B C E 2m 1,6m 15m 0,5m
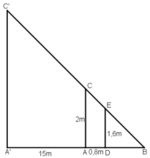
Gọi chiều cao của cây là h = A'C' và cọc tiêu AC = 2m.
Khoảng cách từ chân đến mắt người đo là DE = 1,6m.
Cọc xa cây một khoảng A'A = 15m, và người cách cọc một khoảng AD = 0,8m và gọi B là giao điểm của C'E và A'A.
Ta có: A’C’ ⊥ A’B, AC ⊥ A’B, DE ⊥ A’B
⇒ A’C’ // AC // DE.
Ta có: ΔDEB 
\(\Rightarrow\frac{DE}{AC}=\frac{DB}{AB}\)
Mà AC = 2m , DE = 1,6m
nên \(\frac{1,6}{2}=\frac{DB}{AB}\Rightarrow\frac{DB}{AB}=\frac{4}{5}\Rightarrow\frac{DB}{4}=\frac{AB}{5}\)
Áp dụng t/c DTSBN , ta có:
\(\frac{DB}{4}=\frac{AB}{5}=\frac{AB-DB}{5-4}=\frac{AD}{1}=0,8\)
Suy ra :
\(\frac{DB}{4}=0,8\Rightarrow DB=0,8.4=3,2\)
\(\frac{AB}{5}=0,8\Rightarrow AB=0,8.5=4\)
Mà AB – DB = AD = 0,8
⇒ BD = 0,8.4 =3,2m; AB = 5.0,8 = 4m.
⇒ A'B = A'A + AD + DB = 15 + 0,8 + 3,2 = 19m
+ ΔACB ~ ΔA’C’B (vì AC // A’C’)
\(\Rightarrow\frac{AB}{A'B'}=\frac{AC}{A'C'}\)
\(\Rightarrow AC=\frac{AC.A'B'}{AB}=\frac{2.19}{4}=9,5\left(m\right)\)
Vậy cây cao 9,5m

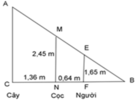
Ta mô tả vị trí cây, cọc và người như hình vẽ bên.
Xét ΔBFE và ΔBNM ta có:
B chung
B E F ^ = B M N ^ (vì EF // MN, cặp góc đồng vị bằng nhau)
=> ΔBFE ~ ΔBNM (g - g)
⇒ B F B N = F E N M ⇔ B F B F + F N = F E N M ⇔ B F B F + 0 , 64 = 1 , 65 2 , 45
⇔ 1,65(BF + 0,64) = 2,45.BF
⇔ BF = 1,32m
Xét ΔBFE và ΔBCA có:
B chung
B E F ^ = B A C ^ (vì EF // AC, cặp góc đồng vị bằng nhau)
=> ΔBFE ~ ΔBCA (g - g)
⇒ B F B C = F E C A ⇔ B F B F + F N + N C = F E C A ⇔ 1 , 32 1 , 32 + 0 , 64 + 1 , 36 = 1 , 65 C A
=> CA = 4,15m
Vậy cây cao đúng bằng độ dài của đoạn CA hay cây cao 4,15m.
Đáp án: D

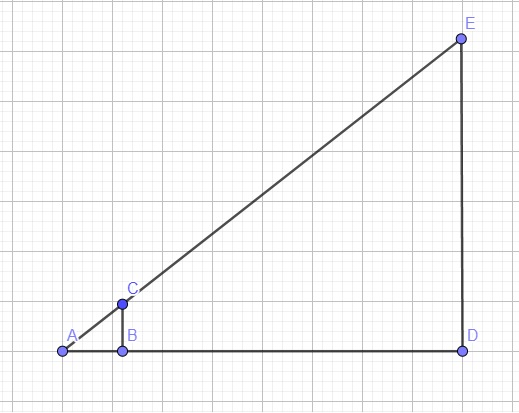
Đặt tên các điểm như hình vẽ.
Ta có \(AB=0,8\left(m\right)\), \(BD=15\left(m\right)\), \(BC=2\left(m\right)\)
Do \(BC||DE\) (cùng vuông góc mặt đất AD)
Áp dụng định lý Thales:
\(\dfrac{AB}{AD}=\dfrac{BC}{DE}\Rightarrow\dfrac{0,8}{0,8+15}=\dfrac{2}{DE}\)
\(\Rightarrow DE=\dfrac{2.15,8}{0.8}=39,5\left(m\right)\)

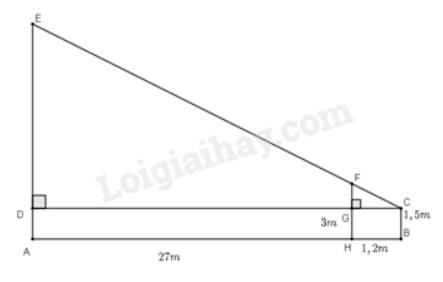
Giả sử, ta biểu diễn người quan sát, cái cọc, tòa nhà có dạng như hình vẽ.
Chiều cao người quan sát là \(CB = 1,5m\); chiều cao cái cọc là \(HF = 3m\); khoảng cách từ người đến cọc là \(HG = 1,2m\); khoảng cách từ tòa nhà đến cọc là \(BH = 27m\). Chiều cao tòa nhà là \(AB\).
Vì tứ giác \(GHBC\) là hình chữ nhật nên \(GC = HB = 1,2m\); Vì tứ giác \(GHAD\) là hình chữ nhật nên \(AH = DG = 27m;GH = AD = 1,5m\).
Chiều dài đoạn \(CD\) là: \(DC = DG + GC = 27 + 1,2 = 28,2m\).
Độ dài đoạn \(GF\) là: \(GF = FH - GH = 3 - 1,5 = 1,5m\)
Xét \(\Delta DEC\) và \(\Delta GFC\) có:
\(\widehat C\) chung
\(\widehat {EDC} = \widehat {FGC} = 90^\circ \)
Do đó, \(\Delta DEC\backsim\Delta GFC\) (g.g)
Vì \(\Delta DEC\backsim\Delta GFC\) nên \(\frac{{DC}}{{GC}} = \frac{{DE}}{{GF}}\) (các cặp cạnh tương ứng)
Thay số, \(\frac{{28,2}}{{1,2}} = \frac{{DE}}{{1,5}} \Rightarrow DE = \frac{{28,2.1,5}}{{1,2}} = 35,25m\)
Chiều cao của tòa nhà là:
\(AD + DE = 35,25 + 1,5 = 36,75m\)
Vậy chiều cao tòa nhà là 36,75m.