Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
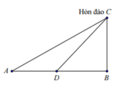
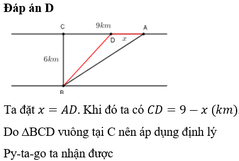
Đặt A D = x ⇒ B D = A B − A D = 40 − x ⇒ C D = B D 2 + B C 2 = 40 − x + 10 2
Suy ra kinh phí người đó phải bỏ là T = 3 x + 5 x 2 − 80 x + 1700 → f x
Khảo sát hàm số f(x)trên (0;40) suy ra min f x = 160 ⇔ x = 65 2 k m
Và chi phí người đó chỉ đi đường thủy là t = 5 40 2 + 10 2 = 500 17 U S D
VẬY kinh phí nhỏ nhất cần bỏ ra khi đi đường bộ là 65/2

Đáp án B.
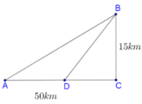
Ta gọi A D = x 0 ≤ x ≤ 50 (km)
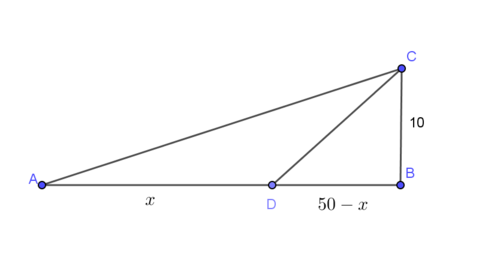
Khi đó: B D = 50 − x ; C D = 100 + 50 − x 2
Từ đó chi phí đi lại là:
f x = 3. x + 5. 100 + 50 − x 2 = 3 x + 5 x 2 − 100 x + 2600
Ta cần tìm để chi phí này là thấp nhất.
Ta có: f ' x = 3 + 5 2 x − 100 2 x 2 − 100 x + 2600 ;
f ' x = 0 ⇔ 6 x 2 − 100 x + 2600 = 500 − 10 x
⇔ x = 42 , 5.
Ta có: f 0 , f 2 < f 42 , 5
Vậy A D = 42 , 5 = 85 2 thì chi phí đi lại là thấp nhất.

Đáp án là D.
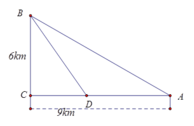
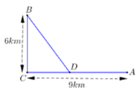
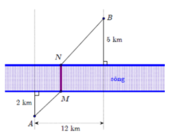
Đặt C D = x , x ∈ 0 ; 9 . Ta có B D = x 2 + 36
Chi phí xây dựng đường ống f x = 100 9 − x + 260 x 2 + 36
Ta có:
f ' x = − 100 + 260 x x 2 + 36 , c h o f ' x = 0 ⇔ 5 x 2 + 36 = 13 x ⇔ x = 5 2
f 0 = 2460 ; f 5 2 = 2340 ; f 9 ≈ 2812 , 33
Chi phí thấp nhất x = 5 2 . Khoảng cách từ A đến D là: 6,5km

Đáp án B
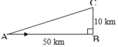
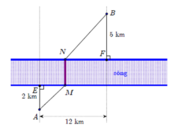
Đặt A D = x → C D = 9 − x suy ra B D = 9 − x 2 + 36 km
Chi phí lắp đặt trên đoạn AD (trên bờ) là T 1 = 100 x triệu đồng
Chi phí lắp đặt trên đoạn DB (dưới nước) là T 2 = 260 9 − x 2 + 36 triệu đồng
Vậy tổng chi phí cần tính là T = T 1 + T 2 = 100 x + 260 9 − x 2 + 36 → f x
Xét hàm số f x = 100 x + 260 x 2 − 18 x + 117 trên đoạn 0 ; 9 → min 0 ; 9 f x = 2340
Dấu = xảy ra khi và chỉ khi x = 13 2 = 6 , 5 km

Đáp án A
Phương pháp: Sử dụng phương pháp hàm số.
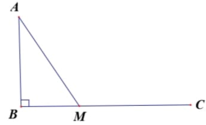
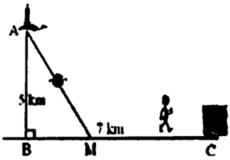
Cách giải: Gọi độ dài đoạn MB là x ![]()
Tam giác ABM vuông tại B => ![]()
Thời gian người đó đi từ A tới C: 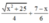
Xét hàm số f(x) 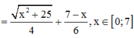

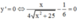
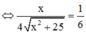
![]()
![]()
=> x = 2 5
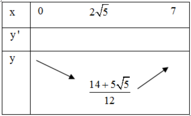
Vậy, để người đó đến C nhanh nhất thì khoảng cách từ B đến M là 2 5

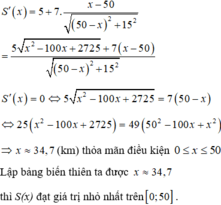





Đáp án B
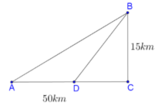
Gọi x (km) là quãng đường bộ mà người đó đi, 0 ≤ x ≤ 50
Suy ra, người đó phải đi với quãng đường thủy là