Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

À rồi, nếu mình hiểu không nhầm thì có nghĩa là \(BB'=6(km)\)
Theo đề bài: Xét tam giác vuông tại $B'$ là $AB'B$ có điểm $M\in AB'$
Đặt $MB'=x$. Chi phí đường ống là: \(AM.5000+13000MB=5000(9-x)+13000\sqrt{36+x^2}\)
Để chi phí min thì \(y=13000\sqrt{36+x^2}-5000x\) phải min.
Có \(y'=\frac{13000x}{\sqrt{36+x^2}}-5000=0\Leftrightarrow x=\pm 2,5\). Do đó $y$ min khi $x=2,5$, tức là $AM=9-2,5=6,5$
Do đó $D$ là đáp án đúng.
Một công ty muốn chạy một đường ống dẫn từ một điểm A trên bờ đến một điểm B trên một hòn đảo mà là 6 km từ bờ biển
Câu bôi đậm có nghĩa gì vậy bạn =)))

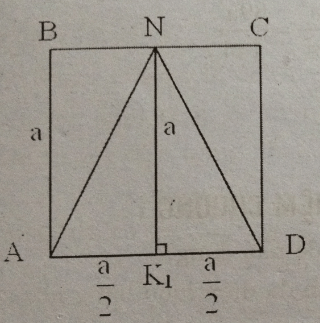
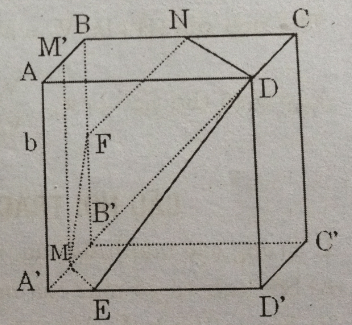
b)-Mặt phẳng (DMN) cắt hình lập phương theo thiết diện MEDNF trong đó ME // ND, FN //DE và chia hình lập phương thành hai khối đa diện (H) và (H’), gọi phần khối lập phương chứa A, B, A’, mặt phẳng (DMN) là (H)
-Chia (H) thành các hình chóp F.DBN, D.ABFMA’ và D.A’EM.

Một đường thẳng muốn vuông góc với một mặt phẳng thì phải vuông góc với 2 đường thẳng chéo nhau chứ bạn? ở ba câu trên bạn mới chứng minh nó vuông với 1 đường mà

S H B K A I C D
Gọi K là hình chiếu của I lên AB
Suy ra \(\widehat{SKI=60^0}\)
Mà \(\frac{BI}{ID}=\frac{BC}{AD}=\frac{a}{3a}=\frac{1}{2}\)\(\Rightarrow\frac{BI}{BI+ID}=\frac{1}{4}\)\(\Rightarrow\frac{BI}{BD}=\frac{1}{4}\)
Suy ra \(\frac{KI}{DA}=\frac{1}{4}\)\(\Rightarrow KI=\frac{3a}{4}\Rightarrow SI=\frac{3a\sqrt{3}}{4}\)
Do \(IK\) \\ \(AD\Rightarrow\frac{KI}{AD}=\frac{BI}{BD}\)
\(V_{A.ABCD}=\frac{1}{3}.SI.S_{ABCD}=\frac{1}{3}.\frac{3a\sqrt{3}}{4}.\frac{1}{2}\left(a+3a\right)a=\frac{a^3\sqrt{3}}{2}\)
Gọi H là hình chiếu của I trên SK. Ta có \(\begin{cases}AB\perp IK\\AB\perp SI\end{cases}\)\(\Rightarrow AB\perp IH\)
Từ đó suy ra \(IK\perp\left(SAB\right)\Rightarrow d\left(I,\left(SAB\right)\right)=IK\)
Mà do \(DB=4IB\Rightarrow\left(D,\left(SAB\right)\right)=4d\left(I,\left(SAB\right)\right)=4IH\)
Lại có \(\frac{1}{IH^2}=\frac{1}{IS^2}+\frac{1}{IK^2}=\frac{16}{27a^2}+\frac{16}{9a^2}=\frac{64}{27a^2}\Leftrightarrow IH=\frac{3a\sqrt{3}}{8}\)
Vậy \(d\left(D,\left(SAB\right)\right)=\frac{3a\sqrt{3}}{2}\)
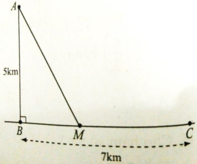


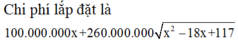
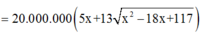

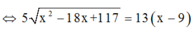
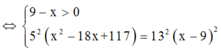




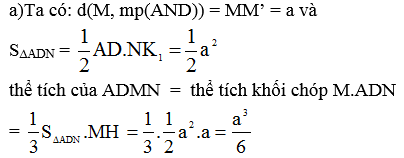
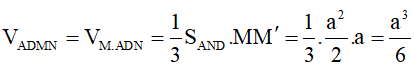



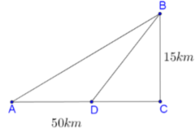

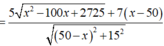



Đặt BM = x (0 ≤ x ≤ 7) => MC = 7 - x. Áp dụng định lí Py-ta-go cho tam giác vuông ABM có
Thời gian đi từ A đến M là
thời gian đi từ M đến C là
Tổng thời gian đi từ A đến C là
Bảng biến thiên
Để người đó đến kho nhanh nhất thì thời gian đi cần ít nhất, tức t đạt giá trị nhỏ nhất. Dựa vào bảng biến thiên ta thấy t đạt giá trị nhỏ nhất tại x = 2√5 ≈ 4,5
Vậy vị trí điểm M cách B một khoảng là 4,5km thì người đó đến kho là nhanh nhất.
Chọn B