Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án : A
Để chọn ba bông hoa có đủ cả ba màu (nghĩa là chọn một bông hoa hồng trắng- một bông hoa hồng đỏ- hoa hồng vàng), ta có:
Có 7 cách chọn hoa hồng trắng.
Có 5 cách chọn hoa hồng đỏ.
Có 6 cách chọn hoa hồng vàng.
Vậy theo qui tắc nhân ta có 7.5.6=210 cách.
Đáp án A.
Hướng dẫn giải:
Số cách lấy 3 bông hồng bất kỳ: 
+ Số cách lấy 3 bông hồng chỉ có một màu:
+ Số cách lấy 3 bông hồng có đúng hai màu:
Vậy số cách chọn thoả yêu cầu bài toán là:
Số cách lấy 3 bông hồng bất kì: 
Số cách lấy 3 bông hồng chỉ có một màu: 
Số cách lấy 3 bông hồng có đúng hai màu: 
Vậy số cách chọn thỏa yêu cầu bài toán là:.2300-211-1529=560
Chọn A.
a. Việc cắm 3 bông hoa vào 3 lọ chính là việc chọn 3 lọ hoa khác nhau từ tập hợp 5 lọ hoa rồi sắp xếp chúng với các bông hoa tương ứng và chính là kết quả của chỉnh hợp chập 3 của 5.
(Vì các bông hoa khác nhau nên mỗi cách sắp xếp cho ta 1 kết quả khác nhau).
Vậy có:
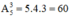(cách).
b. Việc cắm 3 bông hoa giống nhau vào 3 lọ chính là việc chọn 3 lọ hoa khác nhau từ tập hợp 5 lọ hoa để cắm và chính là kết quả của tổ hợp chập 3 của 5.
(Vì các bông hoa giống nhau nên sắp xếp các lọ theo cách nào cũng đều cho cùng một kết quả).
Vậy có:
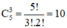(cách).
Việc cắm ba bông hoa vào ba lọ đã cho chính là việc chọn 3 bông hoa trong số 7 bông hoa rồi sắp xếp chúng vào các lọ.
Vậy số cách chọn chính là A 7 3 = 7 . 6 . 5 = 210 (cách).
a) Đánh số thứ tự cho 3 bông hoa. Mỗi cách cắm hoa là một cách chọn ra 3 lọ và sắp thứ tự cho chúng (theo thứ tự của 3 bông hoa), nên mỗi cách cắm là một chỉnh hợp chập 3 của 5 lọ. Suy ra số cách cắm 3 bông hoa vào 5 lọ là:
A35 = 60 (cách).
b) Vì 3 bông hoa là như nhau, nên mỗi cách cắm 3 bông hoa vào 5 lọ khác nhau (mỗi lọ cắm không quá một bông) là một cách chọn ra một tập hợp 3 phần tử (không phân biệt thứ tự) từ 5 lọ. Suy ra số các cách cắm 3 bông hoa như nhau vào 5 lọ khác nhau (mỗi lọ cắm không quá một bông) là:
C35 = = 10 (cách).
Không gian mẫu: \(C_{16}^3\)
a. Số cách chọn 3 bông cùng loại: \(C_5^3+C_7^3+C_4^3=...\)
Xác suất: \(P=\dfrac{C_5^3+C_7^3+C_4^3}{C_{16}^3}=...\)
b. Số cách chọn không có bông nhung nào: \(C_{11}^3\)
Số cách chọn có ít nhất 1 bông nhung: \(C_{16}^3-C_{11}^3\)
Xác suát: \(P=\dfrac{C_{16}^3-C_{11}^3}{C_{16}^3}\)
a: SỐ cách lấy là \(C^3_{15}=455\left(cách\right)\)
b: SỐ cách lấy là \(C^3_4+C^3_5+C^3_6=34\)
c: Số cách lấy là:
4*5*6=60