Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hệ vật "Quả cầu - Lò xo - Trái Đất" là hệ cô lập, do không chịu tác dụng các ngoại lực (lực ma sát, lực cản), chỉ có các nội lực tương tác (trọng lực, phản lực, lực đàn hồi), nên cơ năng của hệ vật bảo toàn.
Chọn vị trí cân bằng của hệ vật làm gốc tính thế năng đàn hồi, chiều lò xo bị kéo dãn là chiều dương.
- Tại vị trí ban đầu : quả cầu có vận tốc v 0 = 0 và lò xo bị kéo dãn một đoạn ∆ l 0 > 0 cm, nên cơ năng của hệ vật:
W 0 = k( ∆ l 0 )2/2
- Tại vị trí cân bằng: quả cầu có vận tốc v ≠ 0 và lò xo không bị biến dạng ( ∆ = 0), nên cơ năng của hệ vật :
W = m v 2 /2
Áp dụng định luật bảo toàn cơ năng cho chuyển động của hệ vật:
W = W 0 ⇒ m v 2 /2 = k( ∆ l 0 )2/2
Suy ra vận tốc của quả cầu khi nó về tới vị trí cân bằng:
v = ∆ l 0 k / m = 3. 10 - 2 100 / 40 . 10 - 3 = 1,5(m/s)

Hệ vật ta xét gồm "Quả cầu - Lò xo - Trái Đất" là hệ cô lập (do không chịu ngoại lực tác dụng) nên cơ năng của hệ vật bảo toàn
Chọn vị trí cân bằng của hệ vật làm gốc tính thế năng đàn hồi, chiều lò xo bị kéo dãn là chiều dương
Tại vị trí ban đầu : quả cầu có vận tốc v0 = 0 và lò xo bị kéo dãn một đoạn Δ∆l0 > 0 cm, nên cơ năng của hệ vật:
\(W_0=\dfrac{k\left(\Delta l_0\right)^2}{2}\)
- Tại vị trí cân bằng: quả cầu có vận tốc v ≠ 0 và lò xo không bị biến dạng (Δ = 0), nên cơ năng của hệ vật :
\(W=\dfrac{mv^2}{2}\)
Áp dụng định luật bảo toàn cơ năng, vận tốc của quả cầu khi nó về tới vị trí cân bằng:
\(W=W_0\Rightarrow\dfrac{mv^2}{2}=\dfrac{k\left(\Delta l_0\right)^2}{2}\Rightarrow v=\Delta l_0\sqrt{\dfrac{k}{m}}=3.10^{-2}.\sqrt{\dfrac{100}{40.10^{-3}}}=1,5\)m/s

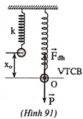
a) Khi m ở vị trí cân bằng O: P → + F d h → = 0 →
Về độ lớn: m g - k x 0 = 0 1
Trong đó x0 là độ giãn lò xo khi vật ở vị trí cân bằng (hình 91). Xét khi m chuyển động, ở vị trí cách O một đoạn x. Thế năng của hệ sẽ bằng công do trọng lực và lực đàn hồi thực hiện khi m di chuyển từ vị trí đang xét trở về vị trí ban đầu ( tức là trở về vị trí cân bằng O).
Ta có:
![]()
hay
![]()
Từ (1) và (2)
![]()
b) Tại vị trí ban đầu ta có
![]()

Bài này theo bảo toàn cơ năng thì độ cao lớn nhất mà vật đạt được so với vị trí cân bằng là 20 cm (bằng độ nén khi ấn xuống)

a/ \(W=\dfrac{1}{2}kx^2+\dfrac{1}{2}mv^2=\dfrac{1}{2}k\Delta l^2\)
\(\Leftrightarrow kx^2+mv^2=k\Delta l^2\Leftrightarrow v=\sqrt{\dfrac{k\Delta l^2-kx^2}{m}}=\sqrt{\dfrac{40.0,02^2-40x^2}{0,4}}\left(m/s\right)\)
b/ \(v_{max}\Leftrightarrow\dfrac{40.0,02^2-40x^2}{0,4}\left(max\right)\Leftrightarrow x=0\) => khi nó ở VTCB
\(\Rightarrow v_{max}=\dfrac{40.0,02^2}{0,4}\left(m/s\right)\)

Đáp án B
Giai đoạn 1:
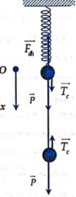
- Sau khi kéo vật B xuống dưới 20 cm và thả nhẹ thì hệ đi lên, hai vật A và B cùng vận tốc, gia tốc đến khi lực căng dây bằng 0.
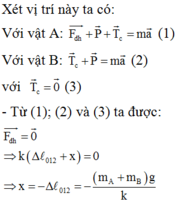
![]()
Giai đoạn 2:
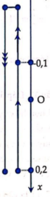
- Dây chùng vật B chuyển động giống như vật được ném thẳng đứng lên trên với vận tốc ban đầu ở giai đoạn này là vận tốc ở cuối giai đoạn (Tc = 0)
- Vận tốc đầu giai đoạn 2 tính từ định luật bảo toàn cơ năng cho con lắc là:
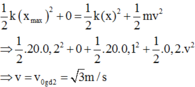
- Quãng đường đi được ở giai đoạn 2 đến khi dừng lại (đạt độ cao lớn nhất) là:
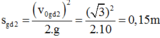
- Kết thúc giai đoạn 2 vật B đã lên đến độ cao so với ban đầu khi buông là:
![]()
Giai đoạn 3:
Vật B tuột khỏi dây từ độ cao 4,5m rơi đến vị trí thả ban đầu là chuyển động rơi tự do, ta có:
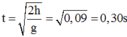

Theo bài ra ta có:
W=Wđ+Wt =1/2.m.v2 +1/2.k.x2= 5.1/2.k.x2
Khi wt =4wđ thì cơ năng ở đó là:
w=wđ+wt = 5/4.wt = 5/4.1/2.kx'2
Theo định luật bảo toàn cơ năng cho hai vị trí ta có:
5/4.1/2.kx'^2 = 5.1/2.k.x^2 -> x' = ...



 10
10
Hệ vật ta xét gồm "Quả cầu - Lò xo - Trái Đất" là hệ cô lập.
Cơ năng W của hệ vật này có giá trị bằng tổng của động năng ( W đ ), thế năng trọng trường ( W t ) và thế năng đàn hồi ( W đ h ) :
W = W đ + W t + W đ h
Chọn gốc toạ độ là vị trí cân bằng của hệ vật (quả cầu đứng yên) và chiều dương là chiều lò xo bị kéo dãn. Do đó ta có :
- Tại vị trí ban đầu : hệ vật có W đ = 0 ( v 0 = 0) lò xo bị dãn một đoạn Δ so với vị trí cân bằng, nên W t ≠ 0, W đ h ≠ 0 và cơ năng của hệ vật bằng :
W 0 = 0 + mg ∆ l + k ∆ l + ∆ l 0 2 /2
- Khi về tới vị trí cân bằng : quả cầu có W đ ≠ 0 (v ≠ 0) và W t = 0 (trùng với gốc tính thế năng đàn hồi), đồng thời lò xo bị dãn một đoạn Δ0, nên cơ năng của hệ vật bằng :
W = m v 2 /2 + 0 + k ∆ l 0 2 /2
Chú ý : Hệ vật này được treo thẳng đứng nên tại vị trí cân bằng của nó, lò xo đã bị dãn một đoạn ∆ 0 thoả mãn điều kiện :
mg + k ∆ 0 = 0 ⇒ mg = -k ∆ 0
với P = mg là trọng lực và F đ h = k ∆ là lực đàn hồi tác dụng lên hệ vật
Áp dụng định luật bảo toàn cơ năng cho hệ vật, ta có :
W = W 0 ⇒ mg ∆ l + k ∆ l + ∆ l 0 2 /2 = m v 2 /2 + k ∆ l 0 2 /2
⇒ mg ∆ l + k ∆ l 2 /2 + k ∆ l ∆ l 0 /2 + k ∆ l 0 2 /2 = m v 2 /2 + k ∆ l 0 2 /2
Vì mg = -k ∆ 0 , nên sau khi rút gọn hai vế của phương trình, ta được
k ∆ l 2 /2 = m v 2 /2
Từ đó suy ra vận tốc của quả cầu khi nó về tới vị trí cân bằng: