Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

sao đang xét tam giác S'IA với S'I'A' lại có tỉ số BA/B'A' vậy ạ

(a)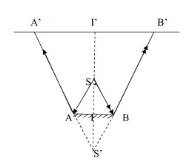
Hình tham khảo, xem \(I\) là \(O\) nhé.
(b) Theo tính chất ảnh qua gương phẳng: \(S'O=SO=80\left(cm\right)\)
Theo đề: \(OO'=4\left(m\right)=400\left(cm\right)\)
\(\Rightarrow S'O'=S'O+OO'=80+400=480\left(cm\right)\)
\(\Delta S'OA\sim\Delta S'O'A':\dfrac{S'O}{S'O'}=\dfrac{S'A}{S'A'}=\dfrac{80}{480}=\dfrac{1}{6}\)
\(\Delta S'AB\sim\Delta S'A'B':\dfrac{S'A}{S'A'}=\dfrac{AB}{A'B'}\)
\(\Leftrightarrow A'B'=AB:\dfrac{S'A}{S'A'}=4:\dfrac{1}{6}=24\left(cm\right)\)
Diện tích hình tròn sáng trên trần nhà: \(S_L=\dfrac{A'B'^2}{4}\pi=\dfrac{24^2}{4}\pi=144\pi\left(cm^2.\right)\)

Cách vẽ:
Gọi: S' là ảnh của S qua gương 1.
\(\Rightarrow\) Tia tới qua gương 1 tạo ra tia phản xạ đi qua S'.
Gọi: S'' là ảnh của S qua gương 2.
\(\Rightarrow\) Tia tới khi qua gương 2 cho tia phản tạo ta tia phản xạ đi qua S
\(\Rightarrow\) Tia tới sẽ đi qua S''.
Giả sử S', S'' cắt G tại A và G' tại B.
\(\Rightarrow\) SABS là đường truyền tia sáng cần vẽ.
Chứng minh:
Ta có: \(\left\{{}\begin{matrix}\widehat{SAG}=\widehat{OAB}\\\widehat{OBA}=\widehat{SBG'}\end{matrix}\right.\)
\(\widehat{ASB}+\widehat{SAB}+\widehat{SBA}=90^0\)
\(\widehat{SAB}+2\widehat{OAB}=180^0\) \(\Rightarrow\widehat{SAB}=180^0-2\widehat{0AB}\)
\(\widehat{SBA}+2\widehat{OAB}=180^0\Rightarrow\widehat{SBA}=180^0-2\widehat{OAB}\)
\(\Rightarrow\widehat{ASB}+180^0-2\widehat{0AB}+180^0-2\widehat{OBA}=180^0\)
\(\Leftrightarrow\widehat{ASB}+2\left(180^0-\widehat{0AB}-\widehat{0BA}\right)=180^0\)
\(\Leftrightarrow\widehat{ASB}+2\alpha=180^0\)
\(\Rightarrow\widehat{ASB}=180^0-2\alpha\)
Vậy \(\widehat{ASB}\) không phụ thuộc vào góc tới mà phụ thuộc vào góc hợp bởi 2 gương (đpcm).
