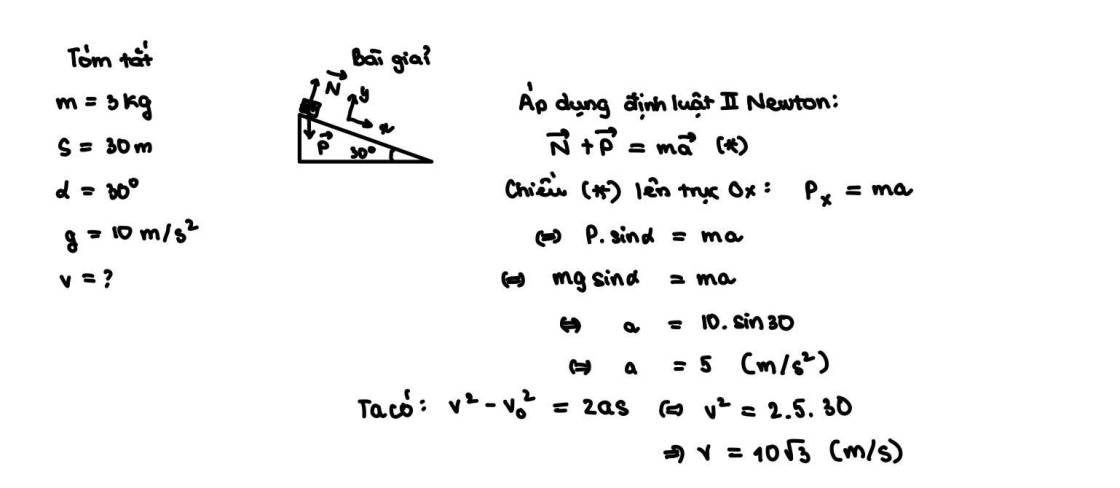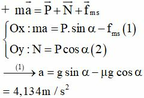Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Từ thế năng trọng trường sang động năng và công của lực ma sát
- Năng lượng có ích: chuyển hoá thành động năng
- Năng lượng hao phí: chuyển hoá thành công lực ma sát
b. Ta có: \(\left\{{}\begin{matrix}W_1=mghsin\alpha=20\cdot10\cdot4\cdot sin30^0=400J\\W_2=\dfrac{1}{2}mv^2=\dfrac{1}{2}\cdot20\cdot4^2=160J\end{matrix}\right.\)
\(\Rightarrow H=\dfrac{W_2}{W_1}100\%=\dfrac{160}{400}100\%=40\%\)

Để tính tốc độ của vật trượt, ta sử dụng công thức:
v = sqrt(2 * g * h)
trong đó:
v là tốc độ của vật (m/s)g là lực trọng (m/s²)h là độ cao của vật từ đỉnh dốc xuống (m)Áp dụng công thức trên vào bài toán:
v = sqrt(2 * 10 * 30) = sqrt(6000) = 75 m/s
Kết quả:
Tốc độ của vật trượt (m/s) = 75 m/sTừ đây, ta có thể nhận thấy tốc độ của vật nặng 3 kg trượt không vận tốc ban đầu từ đỉnh một phẳng nghiêng dài 30 m mặt phẳng nghiêng một góc 30 độ so với phương ngang bỏ qua mọi ma sát và lực cản lấy g=10 m/s² là 75 m/s.

Hình 21.3Ga
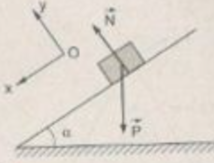
Phương trình chuyển động của vật trên các trục Ox, Oy là
Ox: Psina = ma (1)
Oy : N - Pcosa = 0 (2)
Mặt khác, theo bài ra : a = 2s/ t 2 (3)
Từ (1), (2) và (3) suy ra sin α = a/g = 2s/(g t 2 ) = 2.2,45/(9,8.1) = 0,5
⇒ α = 30 °

\(\left\{{}\begin{matrix}Ox:mg\sin\alpha-F_{ms}=m.a\\Oy:N=mg\cos\alpha\end{matrix}\right.\Rightarrow mg\sin\alpha-\mu mg\cos\alpha=ma\)
\(\Rightarrow a=g\sin\alpha-\mu g\cos\alpha=...\left(m/s^2\right)\)

a) Chọn mốc thế năng tại chân mặt phẳng nghiêng
Ta có: \(h=l.\sin\alpha=\dfrac{1}{2}.2=1\left(m\right)\)
Cơ năng tại A \(W_A=\dfrac{1}{2}mv_A^2+mgz_A=0+mgz_A=5\left(J\right)\)
Bỏ qua ma sát trên mặt phẳng nghiêng cơ năng của vật được bảo toàn: \(W_A=W_B=5\left(J\right)\)
b) Bảo toàn cơ năng: \(W_A=W_B\Leftrightarrow mgz_A=\dfrac{1}{2}mv_B^2\Leftrightarrow v_B=\sqrt{2gz_A}=2\sqrt{5}\left(m/s\right)\)
c) Ta có: \(-F_{ms}=ma\Rightarrow-\mu mg=ma\Rightarrow a=-1\left(m/s^2\right)\)
\(v_C^2-v_B^2=2aS\Rightarrow S=10\left(m\right)\)