Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài này thì có vẹo gì đâu bạn.
\(u=100\sqrt 2\cos(100\pi t)(V)\)
\(Z_L=\omega L = 10\Omega\)
\(Z_C=\dfrac{1}{\omega C}=20\Omega\)
Tổng trở \(Z=\sqrt{r^2+(Z_L-Z_C)^2}=10\sqrt 2 \Omega\)
\(\Rightarrow I_o=\dfrac{U_0}{Z}=10A\)
\(\tan\varphi=\dfrac{Z_L-Z_C}{R}=-1\Rightarrow \varphi=-\dfrac{\pi}{4}\)
Suy ra: \(\varphi=\dfrac{\pi}{4}\)
Vậy \(i=10\cos(100\pi t +\dfrac{\pi}{4})\) (A)

Có: \(L=CR^2=Cr^2\Rightarrow R^2=r^2=Z_LZ_C,URC=\sqrt{3U}_{Lr}\Leftrightarrow Z^2_{RC}=3Z^2_{Lr}\Leftrightarrow R^2+Z^2_C=3\left(Z^2_L+R^2\right)\)
\(\Leftrightarrow-3Z^2_L+Z^2_C=2R^2\) (*) \(R^2=Z_LZ_C\) (**)
Từ (*) và (**) có: \(Z_L=\frac{R}{\sqrt{3}};Z_C=\sqrt{3}R\Rightarrow Z=\sqrt{\left(R+r\right)^2Z^2_{LC}}=\frac{4R}{\sqrt{3}}\Rightarrow\cos\phi=\frac{R+r}{Z}=\frac{\sqrt{3}}{2}\approx0,866\)
A đúng
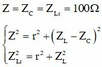
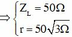
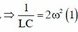
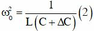
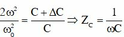
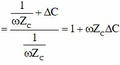
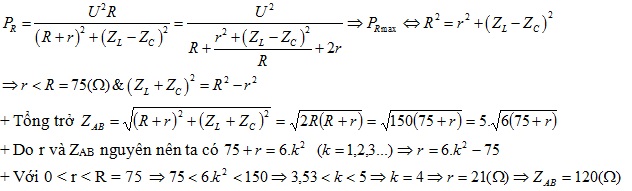
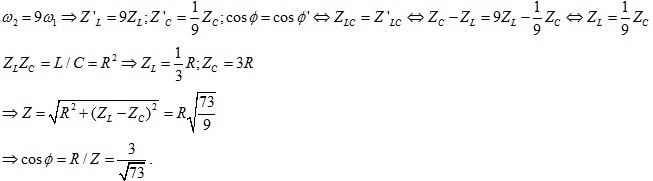
Từ ĐK đầu bài ta có:%5E%7B2%7D%5CRightarrow%20Zc=2Zl=100%5CRightarrow%20%5Comega%20%5E%7B2%7D=%5Cfrac%7B1%7D%7B2LC%7D)
%5E%7B2%7D=%5Cfrac%7B1%7D%7BL(C-%5CDelta%20C)%7D%5CRightarrow%20L.C-L%5CDelta%20C=%5Cfrac%7B1%7D%7B80%5E%7B2%7D.10%7D%5CRightarrow%20%5Cfrac%7B1%7D%7B2%5Comega%5E%7B2%7D%7D-%5Cfrac%7B50%7D%7B%5Comega%20%7D.%5Cfrac%7B0,125.10%5E%7B-3%7D%7D%7B%5CPi%20%7D=%5Cfrac%7B1%7D%7B80%5E%7B2%7D.10%7D)

tần số dao động riwwng của mạch là:
giải phương trình bâc 2 này ra ta được:
Lấy (1) chia (2) ta được: