Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì C ' = 3 C ⇒ Z ' C = Z C 3
Ta có
φ 1 + φ 2 = π 2 ⇒ tan φ 1 tan φ 2 = 1 = Z C − Z L R Z L − Z ' C R = 1 ⇒ Z L − Z ' C = R 2 Z C − Z L
Mặc khác U ' d = 3 U d ⇒ I ' = 3 I ⇔ R 2 + Z C − Z L 2 = 9 R 2 + Z L − Z ' C 2
Thay giá trị Z L − Z ' C = R 2 Z C − Z L ta thu được:
Z C − Z L 4 − 8 R 2 Z C − Z L 2 − 9 R 4 = 0
Giải phương trình
Δ = 64 R 4 + 36 R 4 = 10 R 2 ⇒ Z C − Z L 2 = 9 R 2 Z C − Z L 2 = − R 2 ⇒ Z C − Z L = 3 R Z L − Z ' C = R 3
→ Hệ phương trình trên tương đương với
Z C − Z L = 3 R Z L − Z ' C = R 3 ⇔ Z C − Z L = 3 R Z L − Z C 3 = R 3 ⇒ Z L = 2 R Z C = 5 R
Ta có
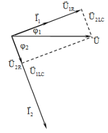
U d U = R 2 + Z L 2 R 2 + Z L − Z C 2 = R 2 + 4 R 2 R 2 + 2 R − 5 R 2 = 2 2 ⇒ U 0 =...

Đáp án B
Phương pháp: Sử dụng định luật Ôm, chú ý điều kiện cộng hưởng.
Cách giải
Khi C = C1, u cùng pha với I, trong mạch có cộng hưởng.
UAB = UR; ULR = 60V
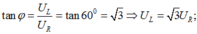
![]()

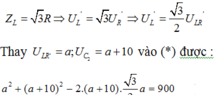
![]()
Chọn đáp án gần giá trị a = 49,86V = 50V

Đáp án B
Phương pháp: Sử dụng định luật Ôm, chú ý điều kiện cộng hưởng.
Cách giải: Khi C = C1, u cùng pha với I, trong mạch có cộng hưởng. UAB = UR; ULR = 60V

![]()
![]()
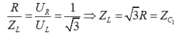
![]()
Khi
C
=
C
2
thì ![]()
Đặt
![]()
. Biết U AB không đổi = 30V, ta có:
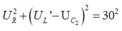
![]()
![]()
Mặt khác,vì
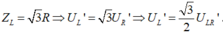
Thay ![]() vào biểu thức (*) ta được:
vào biểu thức (*) ta được:
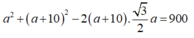
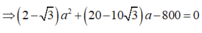
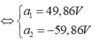
Chọn đáp án gần giá trị a = 49,86V = 50V. Đáp án B

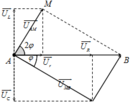
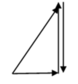
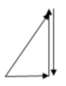
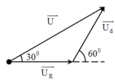
Biễu diễn vecto các điện áp. Mạch xảy ra cộng hưởng → U → cùng phương, chiều với vecto I → . Từ hình vẽ ta có:
U M B = U A M 2 + U 2 − 2 U A M U M B cos 2 φ
Mặc khác, áp dụng định lý sin trong tam giác AMB:
U sin 180 − 3 φ = U A M sin φ → sin 3 φ − 5 4 sin φ = 0
→ 4 sin 3 φ − 7 4 sin φ = 0
Phương trình cho ta nghiệm sin φ = 7 4 → φ ≈ 41 0 .
→ U M B = U A M 2 + U 2 − 2 U A M U M B cos 2 φ ≈ 240 V
Đáp án D

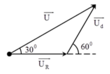
Phương pháp giản đồ vecto.
+ Từ hình vẽ, ta thấy rằng các vecto hợp thành một tam giác cân.
→ U = 2 U d cos 30 0 = 60 3 V
ü Đáp án C
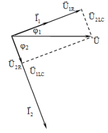
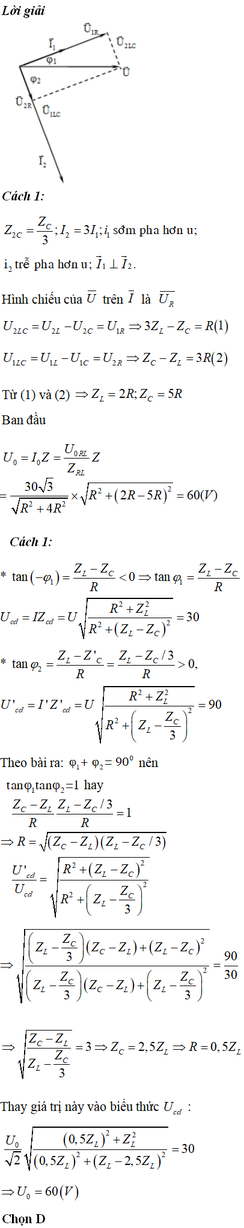


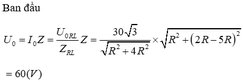

Theo giả thiết, ta có giản đồ véc tơ như sau:
O Z1 Z2 R Zc-ZL ZL-Zc/3 (trước) (sau khi C tăng 3 lần)
Do Ud2 = 3Ud1 nên I2=3.I1 \(\Rightarrow Z_2=\frac{Z_1}{3}\)
Từ giản đồ véc tơ ta có: \(\frac{1}{R^2}=\frac{1}{Z_1^2}+\frac{1}{Z_2^2}=\frac{1}{Z_1^2}+\frac{1}{\left(\frac{Z_1}{3}\right)^2}=\frac{10}{Z_1^2}\Rightarrow Z_1=\sqrt{10}R\)
\(\Rightarrow Z_2=\frac{\sqrt{10}}{3}R\)
\(\begin{cases}Z_1^2=R^2+\left(Z_L-Z_C\right)^2\\Z_2^2=R^2+\left(Z_L-\frac{Z_C}{3}\right)^2\end{cases}\)\(\Rightarrow\begin{cases}10R^2=R^2+\left(Z_L-Z_C\right)^2\\\frac{10}{9}R^2=R^2+\left(Z_L-\frac{Z_C}{3}\right)^2\end{cases}\)\(\Rightarrow Z_L=2R\)
\(\Rightarrow Z_d=\sqrt{5}R\)
Ta có: \(\frac{U_{d1}}{U}=\frac{Z_d}{Z_1}=\frac{\sqrt{5}R}{\sqrt{10}R}=\frac{1}{\sqrt{2}}\)
\(\Rightarrow U=\sqrt{2}U_{d1}=30\sqrt{2}V\)
Đáp án C.
sao I2=3.I1 ạ