

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án C
Con lắc dao động điều hòa theo phương thẳng đứng
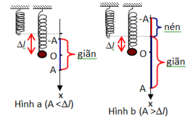
Từ đồ thị => gốc thế năng đàn hồi ở vị trí lò xo có độ dài tự nhiên và thuộc trường hợp A>Δl
Từ đồ thị ta có mỗi dòng ngang có mức thế năng: 0,25 /4 = 0,0625J.
Ta có, thế năng đàn hồi của lò xo: W t = 1 2 k x 2 (x là độ biến dạng của lò xo so với vị trí lò xo có độ dài tự nhiên). Từ đồ thị ta thấy:
+ Tại vị trí lò xo không biến dạng: Wt = 0
+ Tại vị trí vật lên cao nhất: x= A-Δl -> thế năng đàn hồi:
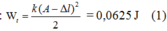
+ Tại vị trí vật xuống thấp nhất:x= A+Δl -> thế năng đàn hồi cực đại :
![]()
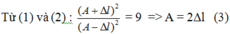
+ Chu kì dao động của con lắc:T= 0,3s
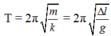
![]()
Suy ra A =2Dl0 = 4,5cm. Từ k ( A - ∆ l ) 2 2 = 0 , 0625
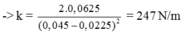
Từ T = 2 π m k
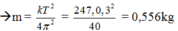

Chọn đáp án C
Tại t = t 2 thì:
W đ 2 = W t 2 = 0,064 J => W = 0,128 J.
Tại t 1 = 0 thì:
W đ 1 = 0,096 J => W t 1 = 0,032 J.
W t W = x a 2 ⇒ x = ± A W t W .
Áp dụng vào hai thời điểm
=> x 1 = ± A 2 . và x 2 = ± A 2 .
Theo bài ra, từ t 1 đến t 2 thì động năng tăng đến giá trị cực đại rồi giảm, tức thế năng của con lắc giảm đến 0 rồi tăng, tương ứng với vật đi từ vị trí x 1 = A 2 . qua vị trí cân bằng, đến x 2 = - A 2 . hoặc ngược lại.
Ta xét 1 trường hợp như trên hình vẽ.
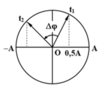
Từ hình vẽ suy ra góc quét:
Δ φ = 5 π 12 ⇒ t = 5 T 24 = π 48
⇒ T = π 10 ⇒ ω = 20 r a d / s
⇒ W = 1 2 m ω 2 A 2 ⇒ A = 8 c m .

Hướng dẫn:
Lực đàn hồi của vật luôn hướng về vị trí lò xo không biến dạng → lực đàn hồi sẽ đổi chiều khi vật đi qua vị trí lò xo không biến dạng (tại vị trí này thế năng đàn hồi bằng 0) → Từ hình vẽ ta thấy trong khoảng thời gian từ t 1 đến t 2 có 2 vị trí thế năng bằng 0 do vậy sẽ có 2 lần lực đàn hồi đổi chiều.
Đáp án B

Đáp án C
Độ biến dạng của lò xo tại vị trí cân bằng
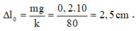
Kéo vật đến vị trí lò xo giãn 7,5 cm rồi thả nhẹ → vật sẽ dao động với biên độ A=5cm.
→ Lực đàn hồi có độ lớn nhỏ nhất khi vật đi qua vị trí lò xo không biến dạng.
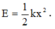
Thế năng của con lắc bằng tổng thế năng đàn hồi và thế năng hấp dẫn. Với gốc thế năng tại vị trí cân bằng thì .
→ Thế năng đàn hồi khi đó có độ lớn
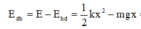
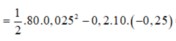
=-0,025J