Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
ü Đáp án C
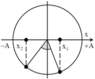
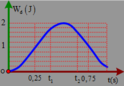
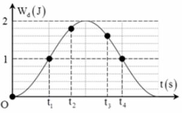
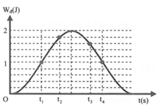
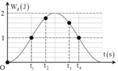
+ Từ đồ thị, ta có:
E d 2 = 9 10 E E d 3 = 8 10 E ⇒ E t 2 = 1 10 E E t 3 = 2 10 E ⇒ x 2 = ± A 10 x 3 = ± A 5
→ Biểu diễn các vị trí tương ứng trên hình tròn, ta thu được:
t 3 - t 2 = T 2 π a r sin x 2 A + a r sin x 3 A = 0 , 25 ⇒ T = 2 s
→ t4 – t1 = 0,25T = 0,5 s
Trong dao động cưỡng bức, biên độ đạt cực đại khi hiện tượng cộng hưởng xảy ra.
Suy ra \(1,25 < f_0 < 1,3\)
→ \(2,5\pi < \omega < 2,6\pi\)
Có \(k = m \omega ^2\) → \(13,3 < k < 14,4\)
→ \(k \approx 13,64 N/m\).
Đáp án C
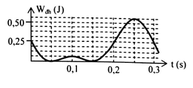
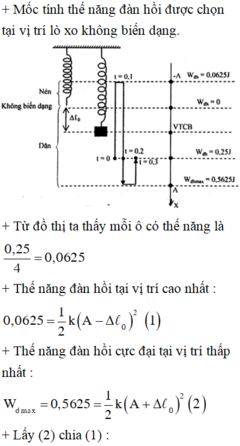
Mốc tính thế năng đàn hồi được chọn tại vị trí lò xo không biến dạng.
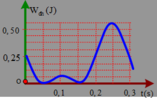
Từ đồ thị ta thấy mỗi ô có thế năng là 0 , 25 4 = 0 , 0625
Thế năng đàn hồi tại vị trí cao nhất: 0 , 0625 = 1 2 k A − Δ l 0 2 ( 1 )
Thế năng đàn hồi cực đại tại vị trí thấp nhất: W d max = 0 , 5625 = 1 2 k A + Δ l 0 2 ( 2 )
Lấy (2) chia (1): 9 = A + Δ l 0 2 A − Δ l 0 2 ⇒ 3 = A + Δ l 0 A − Δ l 0 ⇒ A = 2 Δ l 0 ( 3 )
Từ đồ thị ta thấy chu kì dao động của con lắc là: T = 0 , 3 s
Mặt khác con lắc lò xo treo có chu kì:
T = 2 π m k = 2 π Δ l 0 g ⇒ Δ l 0 = T 2 g 4 π 2 = 0 , 3 2 π 2 4 π 2 = 0 , 0225 m = 2 , 25 c m
⇒ A = 2 Δ l 0 = 4 , 5 c m Thế vào (1): k = 2.0 , 0625 A − Δ l 0 2 = 2.0 , 0625 0 , 045 − 0 , 0225 2 = 247 N / m
⇒ m = T 2 k 4 π 2 = 0 , 3 2 .247 4 π 2 = 0 , 56 k g
Chú ý: Gốc thế năng đàn hồi được chọn tại vị trí lò xo không dãn.
Đáp án C
Trên đồ thị ta có:
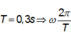
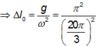
độ biến dạng của lò xo ở VTCB
Chọn chiều dương hướng xuống, gốc tọa độ O tại VTCB, gốc thế năng tại vị trí lò xo không biến dạng. Biểu thức thế năng đàn hồi: 
Từ đó:
- Tại vị trí 
thì
W
t
=
0
- Tại vị trí 
thì 
Tại vị trí 
thì 
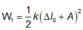
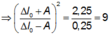
( suy từ các biểu thức thế năng)
Và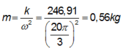 
Đáp án B