Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp: Sử dụng lí thuyết về dao động cưỡng bức
Cách giải :
Theo bài ra tần số góc dao động riêng của CLĐ là:

Khi CLĐ chịu tác dụng của ngoại lực F = F0cos(ωt + π/2) (N) thì nó sẽ dao động với tần số góc bằng tần số góc của ngoại lực. Và khi đó biên độ dao động của CLĐ thay đổi theo tần số góc của ngoại lực theo đồ thị sau:

Theo đề bài khi chu kì dao động của ngoại lực tăng từ 1s lên 3s thì tần số góc của dao động cưỡng bức giảm từ ω1 = 2π(rad/s) xuống ω 2 = 2π/3(rad/s)
Thấy rằng ω1> ω0> ω2 nên khi thay đổi như vậy thì biên độ dao động tăng rồi sau đó giảm

Đáp án D
Phương pháp: Áp dụng công thức tính năng lượng dao động của con lắc đơn
Cách giải:
+ Chiều dài của con lắc đơn: l = T 2 . g 4 π 2 = 2 2 . 9 , 8 4 π 2 = 0 , 993 ( m )
+ Cơ năng dao động của con lắc đơn:
W = 1 2 mglα 0 2 = 1 2 . 0 , 05 . 9 , 8 . 0 , 993 . 0 , 15 2 ≈ 0 , 55 . 10 - 2 ( J )
=> Chọn D

Tần số dao động riêng của con lắc đơn
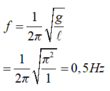
Như vậy khi tần số ngoại lực tăng từ 0,2Hz đến 2Hz thì
+ Từ 0,2Hz đến 0,5Hz thì biên độ dao động tăng
+ Từ 0,5Hz đến 2Hz thì biên độ giảm
Đáp án A

Đáp án A
Tần số dao động riêng của con lắc đơn f = 1 2 π g l = 1 2 π
Như vậy khi tần số ngoại lực tăng từ 0,2Hz đến 2Hz thì
+ Từ 0,2Hz đến 0,5Hz thì biên độ dao động tăng
+ Từ 0,5Hz đến 2Hz thì biên độ giảm

Chọn đáp án C
+ Chu kỳ dao động của con lắc đơn: T = 2 π l g
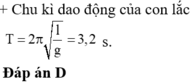
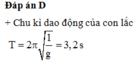
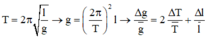
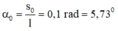
Đáp án B
+ Tần số dao động của con lắc đơn được tính bằng công thức f= 1 2 π g l