Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải:
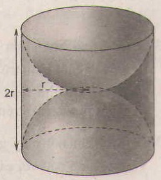
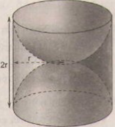
Diện tích phần cần tính gồm diện tích xung quanh hình trụ bán kính đường tròn đáy là r (cm), chiều cao là 2r (cm) và một mặt cầu bán kính r(cm).
Diện tích xung quanh của hình trụ:
Diện tích mặt cầu:
Diện tích cần tính là: +
=

Lời giải:
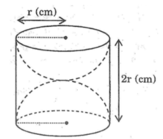
Gọi bán kính đáy khúc gỗ là $r$ (cm) thì:
Thể tích khúc gỗ:
$\pi r^2h=15\pi r^2$ (cm khối)
Thể tích hình nón:
$\frac{1}{3}\pi r^2h=5\pi r^2$ (cm khối)
Thể tích phần bỏ đi:
$15\pi r^2-5\pi r^2=640r$ (cm khối)
$10\pi r^2=640r$
$10\pi r=640$
$r=\frac{64}{\pi}$ (cm)
Thể tích khối nón: $5\pi r^2=5\pi.\frac{64^2}{\pi ^2}=\frac{20480}{\pi}$ (cm khối)
Nghe đề bài có vẻ sai sai. Nếu đề là $640\pi$ (cm khối) thì bạn cũng làm tương tự, $r=8$ (cm)

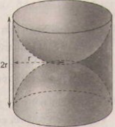
Diện tích toàn bộ của khối gỗ bằng diện tích xung quanh hình trụ cộng với diện tích hai nửa mặt cầu
Diện tích xung quanh hình trụ :
S 1 = 2 π r.h = 2 π r.2r = 4 πr 2 cm 2
Tổng diện tích hai nửa mặt cầu chính là diện tích của hình cầu bán kính r:
S 2 = 4 πr 2 cm 2
Diện tích toàn bộ của khối gỗ :
S = S 1 + S 2 = 4 πr 2 + 4 πr 2 = 8 πr 2 cm 2
Vậy chọn đáp án C


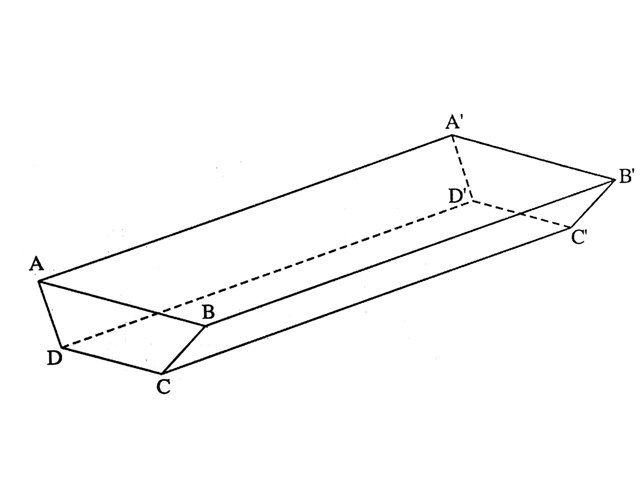
Giả sử ABCD là hình thang cân thỏa điều kiện đề bài.
Hạ đường cao AH, BK xuống BC
Ta tính được DH = \(\frac{CD-AB}{2}=18\left(cm\right)\)
\(\Rightarrow HC=CD-DH=32\left(cm\right)\)
\(\Rightarrow AH=\sqrt{DH.HC}=24\left(cm\right)\)
Từ đó tính được diện tích hình thang ABCD là : \(768cm^2\)
vẽ đườg cao AH&BK.táco:
Tamgiác AHD=támgiacBKC(ccạnh huynề-góc nhọn)
-->DH=KC mà:DC=DH+HK+KC ---->DC=2DH+HK----->DH=(DC-HK):2
mà HK=AB(ABKH là hcn)
dođo:DH=(DC-AB):2=(50-14):2=18
--->HC=32
tamgiác AHD có H^=90dộ theo HTL có:AH^2= DHxHC=18x32=576
--->AH=24
Rùi đó bạn tự tính S hình thang nha!

Diện tích phần cần tính gồm diện tích xung quanh của một hình trụ bán kính đường tròn đáy r (cm), chiều cao là 2r (cm) và một mặt cầu bán kính r (cm).
Diện tích xung quanh của hình trụ:
Sxq = 2πrh = 2πr.2r = 4πr2
Diện tích mặt cầu:
S = 4πr2
Diện tích cần tính là:
4πr2 + 4πr2 = 8πr2

Diện tích phần cần tính gồm diện tích xung quanh của một hình trụ bán kính đường tròn đáy r (cm), chiều cao là 2r (cm) và một mặt cầu bán kính r (cm).
Diện tích xung quanh của hình trụ:
S xq = 2 π rh = 2 π r ⋅ 2 r = 4 π r 2
Diện tích mặt cầu:
S = 4 π r 2
Diện tích cần tính là:
4 π r 2 + 4 π r 2 = 8 π r 2

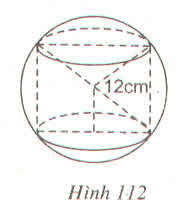
a) Diện tích xung quanh của hình trụ : \(288\pi\left(cm^2\right)\)
b) Thể tích hình cầu : \(2304\pi\left(cm^3\right)\)
c) Diện tích mặt cầu : \(576\pi\left(cm^2\right)\)

Giúp với
Ai đúng phát k luôn
"k" nhầm