Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

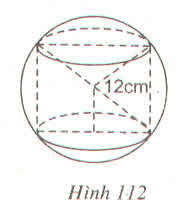
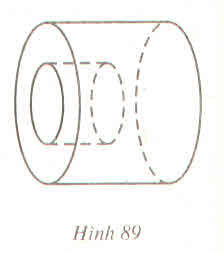
Diện tích phần cần tính gồm diện tích xung quanh của một hình trụ bán kính đường tròn đáy r (cm), chiều cao là 2r (cm) và một mặt cầu bán kính r (cm).
Diện tích xung quanh của hình trụ:
S xq = 2 π rh = 2 π r ⋅ 2 r = 4 π r 2
Diện tích mặt cầu:
S = 4 π r 2
Diện tích cần tính là:
4 π r 2 + 4 π r 2 = 8 π r 2

Giải:
Diện tích phần cần tính gồm diện tích xung quanh hình trụ bán kính đường tròn đáy là r (cm), chiều cao là 2r (cm) và một mặt cầu bán kính r(cm).
Diện tích xung quanh của hình trụ:
Diện tích mặt cầu:
Diện tích cần tính là: +
=

Diện tích phần cần tính gồm diện tích xung quanh hình trụ bán kính đường tròn đáy là r (cm), chiều cao là 2r (cm) và một mặt cầu bán kính r(cm).
Diện tích xung quanh của hình trụ:
\(S_{xq}=2\pi rh=2\pi r.2r=4\pi r^2\)
Diện tích mặt cầu:
\(S=4\pi r^2\)
Diện tích cần tính là:
\(4\pi r^2+4\pi r^2=8\pi r^2\)
DD/s >......

Diện tích toàn bộ của khối gỗ bằng diện tích xung quanh hình trụ cộng với diện tích hai nửa mặt cầu
Diện tích xung quanh hình trụ :
S 1 = 2 π r.h = 2 π r.2r = 4 πr 2 cm 2
Tổng diện tích hai nửa mặt cầu chính là diện tích của hình cầu bán kính r:
S 2 = 4 πr 2 cm 2
Diện tích toàn bộ của khối gỗ :
S = S 1 + S 2 = 4 πr 2 + 4 πr 2 = 8 πr 2 cm 2
Vậy chọn đáp án C

Diện tích cần tính bằng diện tích xung quanh của hình trụ có chiều cao 2r (cm), bán kính đường tròn đáy r (cm) cộng với diện tích mặt cầu bán kính r (cm)
Chọn (C)

a) Với giả thiết ở đề bài, ta có thể tính được r từ đó tính được diện tích mặt cầu gần bằng \(26cm^2\)
b) Tương tự câu a, ta tính được thể tích hình nón là \(7,9cm^3\)

a) Diện tích xung quanh của hình trụ : \(288\pi\left(cm^2\right)\)
b) Thể tích hình cầu : \(2304\pi\left(cm^3\right)\)
c) Diện tích mặt cầu : \(576\pi\left(cm^2\right)\)

Giải:
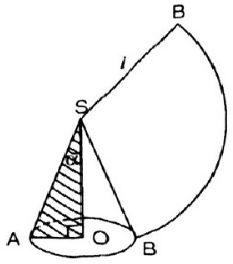
Diện tích hình quạt :
Diện tích xung quanh của hình nón: Sxq = π.r.l
Theo đầu bài ta có: Sxq= Sq => π.r.l=
Vậy l = 4r
Suy ra sin(a) = = 0,25
Vậy a = 14o28’
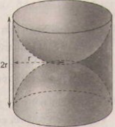
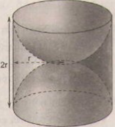
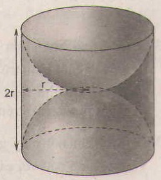
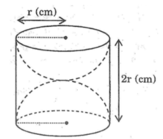

Diện tích phần cần tính gồm diện tích xung quanh của một hình trụ bán kính đường tròn đáy r (cm), chiều cao là 2r (cm) và một mặt cầu bán kính r (cm).
Diện tích xung quanh của hình trụ:
Sxq = 2πrh = 2πr.2r = 4πr2
Diện tích mặt cầu:
S = 4πr2
Diện tích cần tính là:
4πr2 + 4πr2 = 8πr2