Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trả lời:
a) Vận tốc của chuyển động khi t = 2 (s).
Ta có:
v=dsdt=S′=3t2−6t−9v=dsdt=S′=3t2−6t−9
Khi t = 2(s) ⇒ 3.22 – 6.22 – 9 = -9 m/s.
b) Gia tốc của chuyển động khi t = 3(s). Ta có:
a=dvdt=v′=6t−6a=dvdt=v′=6t−6
Ở t = 3(s) ⇒ a = 6.3 – 6 = 12 m/s2
c) Ta có: v = 3t2 – 6t – 9
Tại thời điểm vận tốc triệt tiêu:
v=0⇔3t2−6t−9=0⇔t2−2t−3=0⇔[t=−1(l)t=3(s)v=0⇔3t2−6t−9=0⇔t2−2t−3=0⇔[t=−1(l)t=3(s)
Gia tốc: a = 6t – 6.
Khi t = 3s ⇒ a = 6.3 – 6 = 12 m/s2
d) Ta đã có a = 6t – 6.
Khi a = 0 ⇔ 6t – 6= 0 ⇔ t = 1(s)
Lại có: v = 3t2 – 6t – 9
Khi t = 1(s) ⇒ v = 3.12 – 6.1 – 9 = -12 m/s

a) Vận tốc trung bình của chuyển động trong khoảng thời gian từ t đến t + ∆t là
vtb = =
=
g .(2t + ∆t) ≈ 4,9. (2t + ∆t).
Với t = 5 và
+) ∆t = 0.1 thì vtb ≈ 4,9. (10 + 0,1) ≈ 49,49 m/s;
+) ∆t = 0,05 thì vtb ≈ 4,9. (10 + 0,05) ≈ 49,245 m/s;
+) ∆t = 0,001 thì vtb ≈ 4,9. (10 + 0,001) ≈ 49,005 m/s.
b) Vận tốc tức thời của chuyển động tại thời điểm t = 5s tương ứng với ∆t = 0 nên v ≈ 4,9 . 10 = 49 m/s.

a, Phương trình vận tốc là: v(t) = \(3t^2-6t+8\)
Phương trình gia tốc là: a(t) = \(6t-6\)
Thay t = 3 vào phương trình, ta được:
s = \(3^3-3\cdot3^3+8\cdot3+1=25\left(m\right)\)
\(v=3\cdot3^2-6\cdot3+8=17\left(m/s\right)\\ s=6\cdot3-6=12\left(m/s^2\right)\)
b, Theo đề bài, ta có:
\(t^3-3t^2+8t+1=7\\ \Leftrightarrow t^3-3t^2+8t-6=0\\ \Leftrightarrow\left(t-1\right)\left(t^2-2t+6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}t=1\\t^2-2t+6=0\left(vô.nghiệm\right)\end{matrix}\right.\)
Khi t = 1(s), chất điểm đi được 7m
\(v=3\cdot1^2-6\cdot1+8=5\left(m/s\right)\\ a=6\cdot1-6=0\left(m/s^2\right)\)

S' = 3t2 - 8t - 2. Gia tốc Y(t) = S'' = 6t - 8, Y(3) = 18 - 8 = 10(m/s2)
Chọn đáp án A.

Vận tốc tức thời của chuyển động tại \(t = 2\) là:
\(\begin{array}{l}v\left( 2 \right) = s'\left( 2 \right) = \mathop {\lim }\limits_{t \to 2} \frac{{s\left( t \right) - s\left( 2 \right)}}{{t - 2}} = \mathop {\lim }\limits_{t \to 2} \frac{{\left( {4{t^3} + 6t + 2} \right) - \left( {{{4.2}^3} + 6.2 + 2} \right)}}{{t - 2}}\\ = \mathop {\lim }\limits_{t \to 2} \frac{{4{t^3} + 6t + 2 - 46}}{{t - 2}} = \mathop {\lim }\limits_{t \to 2} \frac{{4{t^3} + 6t - 44}}{{t - 2}} = \mathop {\lim }\limits_{t \to 2} \frac{{2\left( {t - 2} \right)\left( {2{t^2} + 4t + 11} \right)}}{{t - 2}}\\ = \mathop {\lim }\limits_{t \to 2} 2\left( {2{t^2} + 4t + 11} \right) = 2\left( {{{2.2}^2} + 4.2 + 11} \right) = 54\end{array}\)
Vậy vận tốc tức thời của chuyển động lúc \(t = 2\) là: \(v\left( 2 \right) = 54\left( {m/s} \right)\)

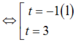
Chọn B
Ta tính được s'(t) = t, do đó vận tốc là v(5) = s'(5) = 5 (m/s)