Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi vận tốc của ca nô khi nước yên lặng là x (km/h) (Điều kiện: x > 2)
Vận tốc của ca nô khi xuôi dòng là: x + 2 (km/h)
Vận tốc của ca nô khi ngược dòng là: x - 2 (km/h)
Thời gian ca nô đi xuôi dòng là: \(\frac{42}{x+2}\left(h\right)\)
Thời gian ca nô đi ngược dòng là: \(\frac{20}{x-2}\left(h\right)\)
Vì tổng thời gian xuôi dòng và nược dòng là 5 giờ do đó ta có phương trình:
\(\frac{42}{x+2}+\frac{20}{x-2}=5\)
Giải phương trình, ta có: \(5x^2-62x+24=0\)
Ta được: \(x=12\) (km/h)
Vậy vận tốc của ca nô khi nước yên lặng là: 12 km/h

Gọi vận tốc của ca nô lúc dòng nước yên lặng là x (km/h); (x > 2)
Vì vận tốc nước là 2 km/h nên vận tốc xuôi dòng và ngược dòng lần lượt là x + 2 và x – 2 (km/h)
Thời gian để ca nô đi hết 42 km xuôi dòng là 42/(x+2) (h)
Thời gian để ca nô đi hết 20 km ngược dòng là 20/(x-2) (h)
Tổng thời gian là 5h do đó
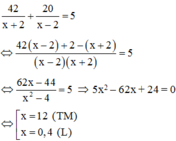
Vậy vận tốc của ca nô khi nước yên lặng là 12 km/h
Đáp án: B

Bài 10:
Gọi số thứ nhất là x(0<x<19)x(0<x<19)
Vậy số thứ hai là 19−x19−x
Theo đề x2+(19−x)2=185⇔x2−19x+88=0x2+(19−x)2=185⇔x2−19x+88=0
Vậy hai số cần tìm là 11 và 8

Vận tốc của ca nô khi xuôi dòng là : 20 : 5 = 4 (km/h)
Vận tốc của ca nô khi nước yên là : 4 - 2 = 2 (km/h)

Gọi vận tốc thực của cano là x(km/h;x>4)
vận tốc xuôi dòng của cano là x+4(km/h)
=> thời gian xuôi dòng của cano là 30/(x+4) (h)
vận tốc ngược dòng của cano là x-4(km/h)
=> thời gian tốc ngược dòng của cano là 30/(x-4) (h)
mà thời gian đi lẫn về của cano là 4 h
=> 30/(x+4)+30/(x-4)=4(chỗ này bạn giải được)
<=> x = 16 và x=-1(loại)
=> vận tốc thực của cano là 16km/h
vậy vận tốc thực của cano là 16km/h