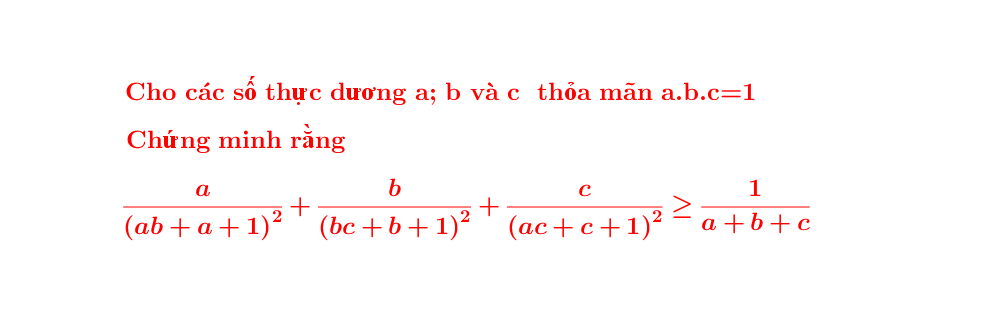Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
GTLN:
Áp dụng BĐT Cauchy-Schwarz:
\(B^2=(6\sqrt{x-1}+8\sqrt{3-x})^2\leq (6^2+8^2)(x-1+3-x)=200\)
\(\Rightarrow B_{\max}= 10\sqrt{2}\Leftrightarrow \frac{3}{\sqrt{x-1}}=\frac{4}{\sqrt{3-x}}\Leftrightarrow x=\frac{43}{25}\)
GTNN:
Ta biết một bổ đề sau: Với \(a,b\geq 0\Rightarrow \sqrt{a}+\sqrt{b}\geq \sqrt{a+b}\)
Cách CM rất đơn giản vì nó tương đương với \(\sqrt{ab}\geq 0\) (luôn đúng)
Áp dụng vào bài toán:
\(\Rightarrow B\geq \sqrt{36x-36+192-64x}=\sqrt{156-28x}\geq 6\sqrt{2}\) (do \(x\leq 3\))
Vậy \(B_{\min}=6\sqrt{2}\Leftrightarrow x=3\)



\(\Leftrightarrow a\sqrt{a}+b\sqrt{b}\ge\left(\sqrt{a}+\sqrt{b}\right)^2\)
\(\Leftrightarrow\left(\sqrt{a}+\sqrt{b}\right)\left(a-\sqrt{ab}+b-\sqrt{a}-\sqrt{b}\right)>=0\)(đúng)

C/m : \(\dfrac{1}{a+2}+\dfrac{1}{b+2}+\dfrac{1}{c+2}=1\) (*)
Thật vậy , (*) \(\Leftrightarrow\left(a+2\right)\left(b+2\right)+\left(b+2\right)\left(c+2\right)+\left(a+2\right)\left(c+2\right)=\left(a+2\right)\left(b+2\right)\left(c+2\right)\)
\(\Leftrightarrow ab+bc+ac+4\left(a+b+c\right)+12=abc+2\left(ab+bc+ac\right)+4\left(a+b+c\right)+8\)
\(\Leftrightarrow ab+bc+ac+abc=4\) (Đ)
=> (*) đúng ( đpcm )

\(vp=\frac{a\left(1+b\right)+b\left(1+a\right)}{\left(1+a\right)\left(1+b\right)}=\frac{2ab+a+b}{1+ab+a+b}\)
\(\ge\frac{a+b}{1+ab+a+b}\)
\(\ge\frac{a+b}{1+a+b}\)