Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:P=(\(\frac{3a}{b+c}\)\(\frac{3a}{b+c}\)+3)+(\(\frac{4b}{a+c}\)+4)+(\(\frac{5c}{a+b}\)+5)-12
P=(a+b+c)(\(\frac{3}{b+c}\)+\(\frac{4}{c+a}\)+\(\frac{5}{a+b}\))-12
Áp dụng BĐT Bunhiacopxki
P=\(\frac{1}{2}\)((b+c)+(c+a)+(a+b))(\(\frac{3}{b+c}\)+\(\frac{4}{c+a}\)+\(\frac{5}{a+b}\))-12\(\ge\)\(\frac{\left(\sqrt{3}+2+\sqrt{5}\right)^2}{2}\)-12
Dấu''='' xảy ra \(\Leftrightarrow\)\(\frac{b+c}{\sqrt{3}}\)=\(\frac{c+a}{2}\)=\(\frac{a+b}{\sqrt{5}}\)

Lời giải:
\(a+b+c+abc-ab-bc-ac-1>0\)
\(\Leftrightarrow (a+b-ab-1)+c(ab-a-b+1)>0\)
\(\Leftrightarrow (a+b-ab-1)-c(a+b-ab-1)>0\)
\(\Leftrightarrow (a+b-ab-1)(1-c)>0\)
\(\Leftrightarrow [a(1-b)-(1-b)](1-c)>0\)
\(\Leftrightarrow (a-1)(1-b)(1-c)>0\Leftrightarrow (a-1)(b-1)(c-1)>0\)
Người ta biến đổi tắt thôi bạn.


Câu 13:
Ta có: \(f\left(x\right)>0\Leftrightarrow3x-m>0\Leftrightarrow3x>m\)
Mà x>1 hay 3x>3
Vậy \(m\le3\)
Đáp án C
Câu 14:
(d): x-2y+1=0 hay \(\dfrac{1}{2}x+\dfrac{1}{2}=y\)
Gọi phương trình đường thẳng cần tìm là: y=ax+b
Phương trình cần tìm đi qua A nên ta có: 2=-2a+b
Để phương trình cần tìm vuông góc với (d) thì: \(a.\dfrac{1}{2}=-1\Rightarrow a=-2\)\(\Rightarrow b=-2\)
Vậy phương trình cần tìm là: \(y=-2x-2\)
Đáp án C

Nhận thấy \(cos\frac{x}{2}=0\) ko phải nghiệm, chia 2 vế cho \(cos^3\frac{x}{2}\) ta được:
\(3tan^3\frac{x}{2}+3tan^2\frac{x}{2}=tan\frac{x}{2}+1\)
\(\Leftrightarrow3tan^2\frac{x}{2}\left(tan\frac{x}{2}+1\right)-\left(tan\frac{x}{2}+1\right)=0\)
\(\Leftrightarrow\left(3tan^2\frac{x}{2}-1\right)\left(tan\frac{x}{2}+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tan\frac{x}{2}=-1\\tan\frac{x}{2}=\frac{1}{\sqrt{3}}\\tan\frac{x}{2}=-\frac{1}{\sqrt{3}}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\frac{\pi}{2}+k2\pi\\x=\frac{\pi}{3}+k2\pi\\x=-\frac{\pi}{3}+k2\pi\end{matrix}\right.\)
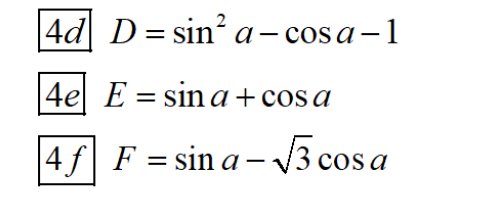
 Giúp mình từ 13 -> 16 nhé. Mình cảm ơn
Giúp mình từ 13 -> 16 nhé. Mình cảm ơn
\(\Leftrightarrow a\sqrt{a}+b\sqrt{b}\ge\left(\sqrt{a}+\sqrt{b}\right)^2\)
\(\Leftrightarrow\left(\sqrt{a}+\sqrt{b}\right)\left(a-\sqrt{ab}+b-\sqrt{a}-\sqrt{b}\right)>=0\)(đúng)
em cảm ơn :>>>