
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét ΔAMB có
MD là đường phân giác ứng với cạnh AB
nên \(\dfrac{AD}{DB}=\dfrac{AM}{MB}\)(1)
Xét ΔAMC có
ME là đường phân giác ứng với cạnh AC
nên \(\dfrac{AE}{EC}=\dfrac{AM}{MC}\)(2)
Ta có: M là trung điểm của BC(gt)
nên MB=MC(3)
Từ (1), (2) và (3) suy ra \(\dfrac{AD}{DB}=\dfrac{AE}{EC}\)
hay DE//BC(đpcm)

Xét tam giác ABC vuông cân có:
\(BC^2=AB^2+AC^2=2AB^2=200\Rightarrow BC=10\sqrt{2}\)(cm)
P△ABC=AB+AC+BC=10.2+10=30(cm)
S△ABC=\(\dfrac{1}{2}AB.AC=\dfrac{1}{2}.10.10=50\left(cm^2\right)\)
Cho mình sửa lại: PΔABC=AB+AC+BC=\(10.2+10\sqrt{2}=20+10\sqrt{2}\left(cm\right)\)

a: Xét ΔAHB vuông tại H và ΔCHA vuông tại H có
góc HAB=góc HCA
=>ΔAHB đồng dạng với ΔCHA
b,c: góc FAE+góc FHE=180 độ
=>FAEH nội tiếp
=>góc HFE=góc HAE=góc C
Xét ΔHFE vuông tại H và ΔHCA vuông tại H có
góc HFE=góc HCA
=>ΔHFE đồng dạng với ΔHCA
=>HF/HC=HE/HA
=>HF*HA=HC*HE





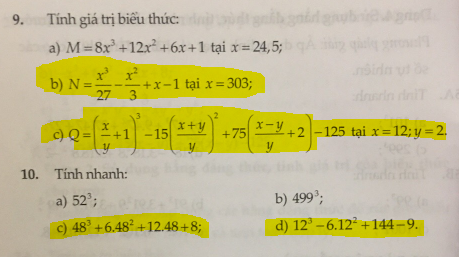 Mọi người ơi giúp em với ạ. Mai em phải nộp rồi. Mấy phần em đánh dấu đó mọi người.
Mọi người ơi giúp em với ạ. Mai em phải nộp rồi. Mấy phần em đánh dấu đó mọi người. 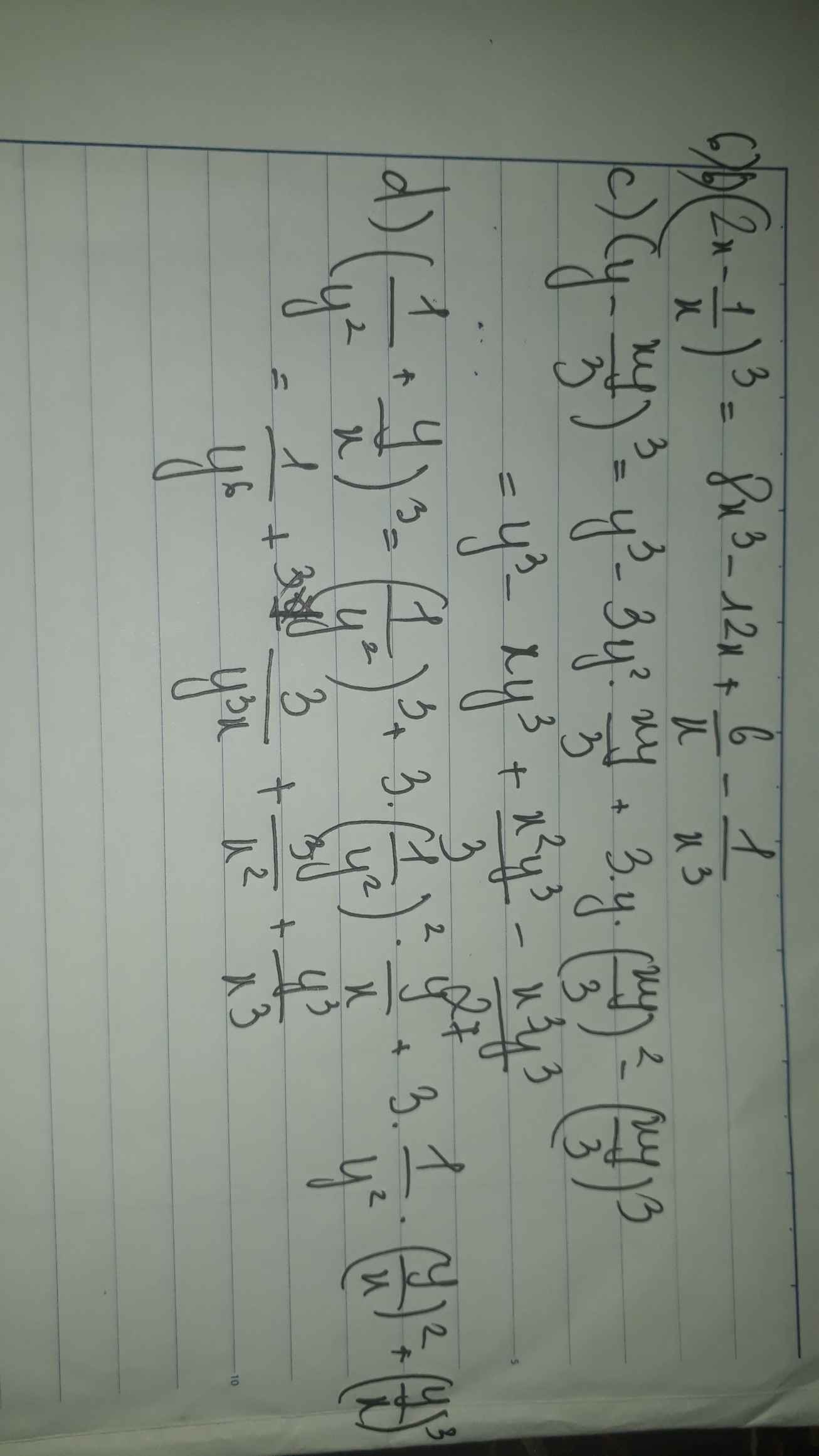
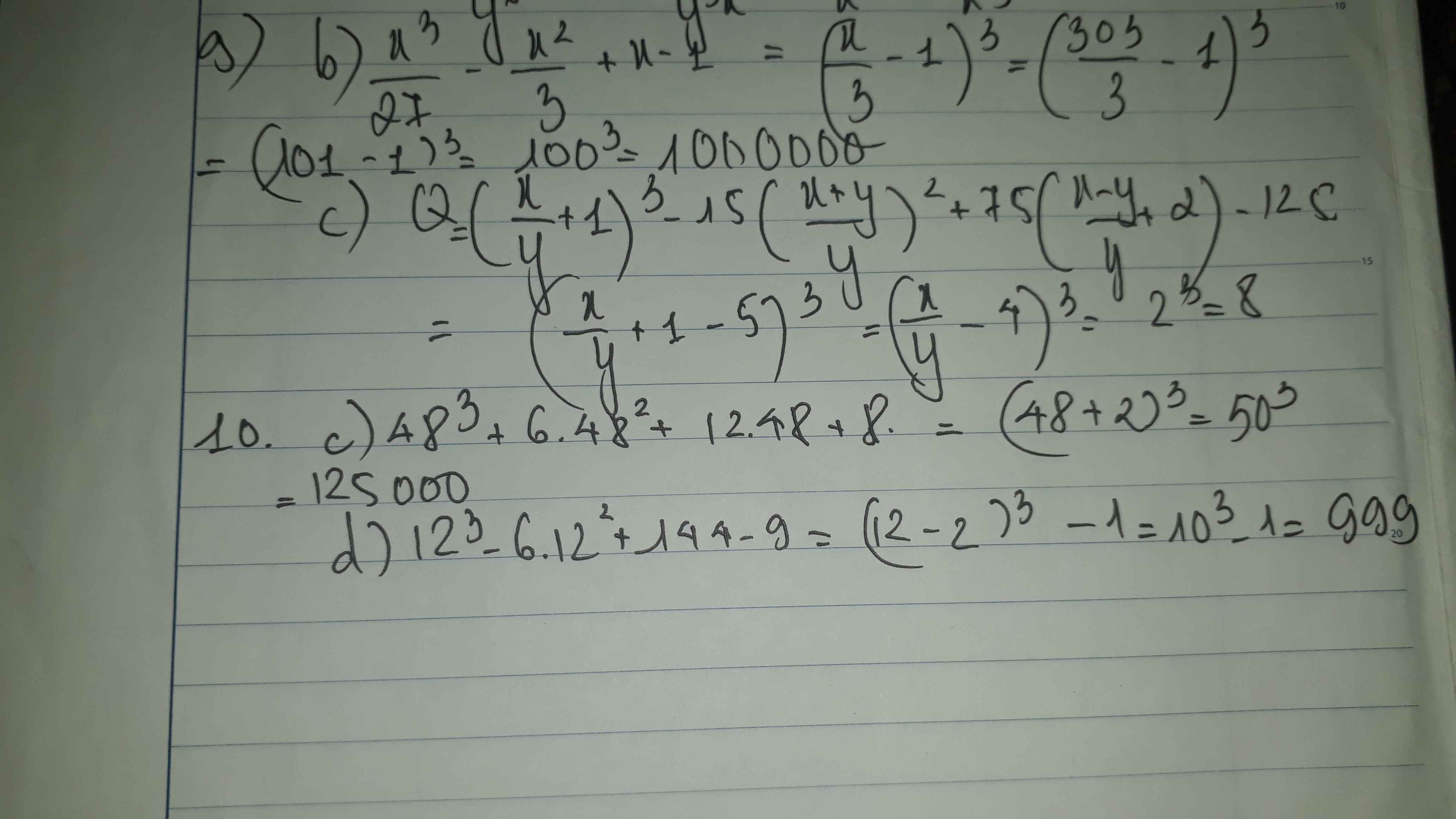
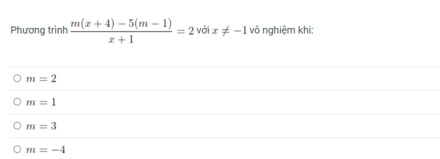







2x - 6y
= 2 ( x - 3y )
4x + 8
= 4 ( x + 2 )