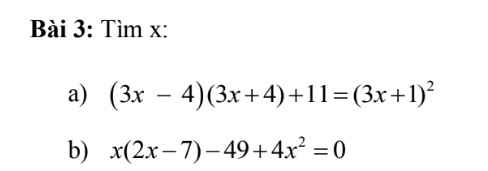K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NM
Nguyễn Minh Quang
Giáo viên
3 tháng 9 2021
Mình làm 1 bài thôi nhé
Bài 5
\(a.1-2y+y^2=\left(1-y\right)^2\)
\(b.\left(x+1\right)^2-25=\left(x+1\right)^2-5^2=\left(x-4\right)\left(x+6\right)\)
\(c.1-4x^2=1-\left(2x\right)^2=\left(1-2x\right)\left(1+2x\right)\)
\(d.27+27x+9x^2+x^3=3^3+3.3^3.x+3.3.x^2+x^3=\left(3+x\right)^3\)
\(f.8x^3-12x^2y+6xy-y^3=\left(2x\right)^3-3.\left(2x\right)^2.y+3.2x.y-y^3=\left(2x-y\right)^3\)
3 tháng 9 2021
Bài 4 :
a, \(x^3+3x^2-x-3=x^2\left(x+3\right)-\left(x+3\right)=\left(x+1\right)\left(x-1\right)\left(x+3\right)\)
b, bạn xem lại đề nhé
c, \(x^2-4x+4-y^2=\left(x-2\right)^2-y^2=\left(x-2-y\right)\left(x-2+y\right)\)
d, \(5x+5-x^2+1=5\left(x+1\right)+\left(1-x\right)\left(x+1\right)=\left(x+1\right)\left(6-x\right)\)
6 tháng 12 2021
b: \(\Leftrightarrow\left(2x-7\right)\left(3x+7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=-\dfrac{7}{3}\end{matrix}\right.\)
13 tháng 11 2021
a: Xét tứ giác AEDF có
AE//DF
AF//DE
Do đó: AEDF là hình bình hành
mà \(\widehat{DAE}=90^0\)
nên AEDF là hình chữ nhật
10 tháng 10 2021
Bài 2:
a: Xét ΔEHK và ΔGFI có
\(\widehat{EHK}=\widehat{GFI}\)
EH=GF
\(\widehat{E}=\stackrel\frown{G}\)
Do đó: ΔEHK=ΔGFI
Suy ra: EK=GI và KH=IF
Ta có: EK+KF=EF
GI+IH=GH
mà EF=GH
và EK=GI
nên KF=IH
Xét tứ giác FKHI có
FK=HI
HK=FI
Do đó: FKHI là hình bình hành
8 tháng 6 2021
a)Đk:\(x\ne4\)
\(\dfrac{x^4}{4-x}+x^3+1=\dfrac{x^4+\left(x^3+1\right)\left(4-x\right)}{4-x}\)\(=\dfrac{x^4+\left(-x^4+4x^3+4-x\right)}{4-x}=\dfrac{4x^3-x+4}{4-x}\)
b) Đk: \(x\ne0;x\ne1\)
\(\dfrac{1}{x^2-x}+\dfrac{2x}{x-1}=\dfrac{1}{x\left(x-1\right)}+\dfrac{2x^2}{x\left(x-1\right)}=\dfrac{1+2x^2}{x\left(x-1\right)}\)
KY
4
XO
17 tháng 7 2021
a) x12 + 4 = x12 + 4x6 + 4 - 4x6 = (x6 + 2)2 - (2x3)2
= (x6 - 2x3 + 2)(x6 + 2x3 + 2)
b) 4x8 + 1 = 4x8 + 4x4 + 1 - 4x4 = (2x4 + 1)2 - (2x2)2
= (2x4 + 2x2 + 1)(2x4 - 2x2 + 1)
17 tháng 7 2021
c) x7 + x5 - 1 = x7 - x + x5 + x2 - (x2 - x + 1) = x(x6 - 1) + x2(x3 + 1) - (x2 - x + 1)
= x(x3 - 1)(x3 + 1) + x2(x + 1)(x2 - x + 1) - (x2 - x + 1)
= (x4 - x)(x + 1)(x2 - x + 1) + (x3 + x2)(x2 - x + 1) - (x2 - x + 1)
= (x5 + x4 - x2 - x + x3 + x2 - 1)(x2 -x + 1)
= (x5 + x4 + x3 - x - 1)(x2 - x + 1)
d) x7 + x5 + 1 = x7 - x + x5 - x2 + (x2 + x + 1)
= x(x3 - 1)((x3 + 1) + x2(x3 - 1) + (x2 + x + 1)
= (x4 + x)(x - 1)(x2 + x + 1) + x2(x - 1)((x2 + x + 1) + (x2 + x + 1)
= (x2 + x + 1)(x5 - x4 + x2 - x + x3 - x2 + 1)
= (x2 + x + 1)(x5 - x4 + x3 - x + 1)
LT
1
