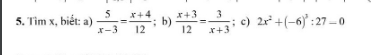Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

B1: Giải:
Vì DE song song với BC => góc DIB= góc IBC (SLT).Mà góc IBC=góc DBI (BI là (p/g của góc ABC ) => góc DBI=góc DIB theo định lý => tam DIB cân tại D=>DB=DI.
Vì DE song song với BC=>góc EIC = góc ICB (SLT). Mà góc ECI =góc ICB ( CI là p/g của của góc ECB) theo định lý => tam giác IEC cân tại E=>EI=EC.
Vì DE=DB+IE. Mà DI = DB;IE=EC=>DE=DB+CE
Vậy : DE=DB+CE

A B E D C K
a) Xét \(\Delta BAE,\Delta BDE\) có :
\(BE:Chung\)
\(\widehat{BAE}=\widehat{BDE}\left(=90^o\right)\)
\(BA=BD\left(gt\right)\)
=> \(\Delta BAE=\Delta BDE\left(c.g.c\right)\)
=> EA = ED (2 cạnh tương ứng)
b) Hình vẽ
Ta nối từ điểm B đến điểm E .
Xét \(\Delta ABE\perp A\) và \(\Delta DBE\perp D\) có :
BA = BD (gt)
BE : cạnh chung
\(\Rightarrow\Delta ABE=\Delta DBE\left(c.h-c.g.v\right)\)
\(\Rightarrow\) AE = ED

a) \(\Rightarrow\left(x-3\right)\left(x+4\right)=5.12\)
\(\Rightarrow x^2+x-72=0\)
\(\Rightarrow\left(x-8\right)\left(x+9\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=8\\x=-9\end{matrix}\right.\)
b) \(\Rightarrow\left(x+3\right)^2=36\)
\(\Rightarrow\left[{}\begin{matrix}x+3=6\\x+3=-6\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=3\\x=-9\end{matrix}\right.\)
c) \(\Rightarrow2x^2=8\Rightarrow x^2=4\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)


Bài làm
a) Ta có: \(\widehat{ABC}+\widehat{ABD}=180^0\)( Hai góc kề bù )
\(\widehat{ACB}+\widehat{ACE}=180^0\)( Hai góc kề bù )
Mà \(\widehat{ABC}=\widehat{ACB}\)( Do tam giác ABC cân ở A )
=> \(\widehat{ABD}=\widehat{ACE}\)
Xét tam giác ABD và tam giác ACE có:
AB = AC ( Do tam giác ABC cân ở A )
\(\widehat{ABD}=\widehat{ACE}\)( cmt )
BD = CE ( gt )
=> Tam giác ABD = tam giác ACE ( c.g.c )
=> AD = AE ( hai cạnh tương ứng )
b) Ta có:
BD + BM = DM
CE + CM = EM
Mà DB = CE ( gt ), BM = CM ( Do M là trung điểm )
=> DM = EM
Xét tam giác AMD và tam giác AME có:
AD = AE ( cmt )
AM chung
DM = EM ( cmt )
=> Tam giác AMD = tam giác AME ( c.c.c )
=> \(\widehat{DAM}=\widehat{EAM}\)( Hai góc tương ứng )
b) Vì tam giác ABD = tam giác ACE ( cmt )
=> \(\widehat{ADB}=\widehat{ACE}\)( Hai góc tương ứng )
Xét tam giác BHD và tam giác CKE có:
\(\widehat{BHD}=\widehat{CKE}\left(=90^0\right)\)
Cạnh huyền: BD = CE ( gt )
Góc nhọn: \(\widehat{ADB}=\widehat{ACE}\)( cmt )
=> Tam giác BHD = tam giác CKE ( cạnh huyền - góc nhọn )
=> BH = CK ( hai cạnh tương ứng )
# Học tốt #

A B C H K I
a) Xét \(\Delta ABH,\Delta ACK\) có :
\(\widehat{A}:Chung\)
\(AB=AC\) (\(\Delta ABC\) cân tại A)
\(\widehat{AHB}=\widehat{AKC}\left(=90^o\right)\)
=> \(\Delta ABH=\Delta ACK\) (cạnh huyền - góc nhọn)
=> \(BH=CK\) (2 cạnh tương ứng)
b) Xét \(\Delta KBC,\Delta HCB\) có :
\(\widehat{KBC}=\widehat{HCB}\) (\(\Delta ABC\) cân tại A)
\(BC:Chung\)
\(\widehat{BKC}=\widehat{CHB}\left(=90^o\right)\)
=> \(\Delta KBC=\Delta HCB\) (cạnh huyền - góc nhọn)
=> \(BK=HC\) (2 cạnh tương ứng)
Xét \(\Delta KIB,\Delta HIC\) có :
\(\widehat{KBI}=\widehat{HCI}\) (\(\Delta ABH=\Delta ACK\))
\(BK=HC\left(cmt\right)\)
\(\widehat{BKI}=\widehat{CHI}\left(=90^o\right)\)
=> \(\Delta KIB=\Delta HIC\left(g.c.g\right)\)
=> IH = IK (2 cạnh tương ứng)