
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




\(\dfrac{1+x}{1-x}+3=\dfrac{x-3}{x-1}\)
\(ĐK:x\ne1\)
\(\Leftrightarrow\dfrac{1+x}{1-x}+3=\dfrac{3-x}{1-x}\)
\(\Leftrightarrow\dfrac{\left(1+x\right)+3\left(1-x\right)}{1-x}=\dfrac{3-x}{1-x}\)
\(\Leftrightarrow\left(1+x\right)+3\left(1-x\right)=3-x\)
\(\Leftrightarrow1+x+3-3x=3-x\)
\(\Leftrightarrow-x=-1\)
\(\Leftrightarrow x=1\left(ktm\right)\)
Vậy pt vô nghiệm
\(\dfrac{1+x}{1-x}+3=\dfrac{x-3}{x-1}\) đề như thế này phải ko?
Mọi người giải giúp mình bài này với ạ, cảm ơn mn nhiều, chỉ cần câu c ý chứng minh góc 90 độ thôi ạ

a: Xét tứ giác ABQN có
\(\widehat{BQN}=\widehat{QNA}=\widehat{NAB}=90^0\)
=>ABQN là hình chữ nhật
b: Xét ΔCAD có
DN,CH là các đường cao
DN cắt CH tại M
Do đó: M là trực tâm của ΔCAD
=>AM\(\perp\)CD
c: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
\(\widehat{HAB}=\widehat{HCA}\left(=90^0-\widehat{ABC}\right)\)
Do đó: ΔHAB đồng dạng với ΔHCA
=>\(\dfrac{HA}{HC}=\dfrac{HB}{HA}\)
=>\(HA^2=HB\cdot HC\)
=>\(HA=\sqrt{HB\cdot HC}\)

a) x^2 - x = 0
x(x-1)=0
x=0 hoặc x=1
b) (x-2)^2 - 3(x-2)=0
(x-2)(x-5)=0
x=2 hoặc x=5
c) pt <=> 3(x - 1) - 2(x - 1)=0
<=> x-1=0
<=> x = 1
a) \(\Rightarrow x\left(x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
b) \(\Rightarrow\left(x-2\right)\left(x-5\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=5\end{matrix}\right.\)
c) \(\Rightarrow3\left(x-1\right)-2\left(x-1\right)=0\)
\(\Rightarrow x-1=0\Rightarrow x=1\)
d) \(\Rightarrow\left(x-5\right)\left(x+5\right)+\left(x-5\right)^2=0\)
\(\Rightarrow\left(x-5\right).2x=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=5\end{matrix}\right.\)
e) \(\Rightarrow\left(x-1\right)\left(x+1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)

\(\Leftrightarrow x^2-6x+9-x^2+4=1\)
=>-6x=-12
hay x=2

Câu 10:
a: ĐKXĐ: \(\left\{{}\begin{matrix}x\notin\left\{2;-1\right\}\\y\ne-5\end{matrix}\right.\)
\(A=\dfrac{y+5}{x^2-4x+4}\cdot\dfrac{x^2-4}{x+1}\cdot\dfrac{x-2}{y+5}\)
\(=\dfrac{y+5}{y+5}\cdot\dfrac{\left(x^2-4\right)}{x^2-4x+4}\cdot\dfrac{x-2}{x+1}\)
\(=\dfrac{\left(x^2-4\right)\cdot\left(x-2\right)}{\left(x+1\right)\left(x^2-4x+4\right)}\)
\(=\dfrac{\left(x+2\right)\left(x-2\right)\cdot\left(x-2\right)}{\left(x+1\right)\left(x-2\right)^2}=\dfrac{x+2}{x+1}\)
b: \(A=\dfrac{x+2}{x+1}\)
=>A không phụ thuộc vào biến y
Khi x=1/2 thì \(A=\left(\dfrac{1}{2}+2\right):\left(\dfrac{1}{2}+1\right)=\dfrac{5}{2}:\dfrac{3}{2}=\dfrac{5}{2}\cdot\dfrac{2}{3}=\dfrac{5}{3}\)
Câu 12:
a: \(A=\dfrac{x}{x+3}+\dfrac{2x}{x-3}+\dfrac{9-3x^2}{x^2-9}\)
\(=\dfrac{x}{x+3}+\dfrac{2x}{x-3}+\dfrac{9-3x^2}{\left(x+3\right)\left(x-3\right)}\)
\(=\dfrac{x\left(x-3\right)+2x\left(x+3\right)+9-3x^2}{\left(x+3\right)\left(x-3\right)}\)
\(=\dfrac{x^2-3x+2x^2+6x+9-3x^2}{\left(x+3\right)\left(x-3\right)}\)
\(=\dfrac{3x+9}{\left(x+3\right)\left(x-3\right)}=\dfrac{3\left(x+3\right)}{\left(x+3\right)\left(x-3\right)}=\dfrac{3}{x-3}\)
b: Khi x=1 thì \(A=\dfrac{3}{1-3}=\dfrac{3}{-2}=-\dfrac{3}{2}\)
\(x+\dfrac{1}{3}=\dfrac{10}{3}\)
=>\(x=\dfrac{10}{3}-\dfrac{1}{3}\)
=>\(x=\dfrac{9}{3}=3\left(loại\right)\)
Vậy: Khi x=3 thì A không có giá trị
c: \(B=A\cdot\dfrac{x-3}{x^2-4x+5}\)
\(=\dfrac{3}{x-3}\cdot\dfrac{x-3}{x^2-4x+5}\)
\(=\dfrac{3}{x^2-4x+5}\)
\(x^2-4x+5=x^2-4x+4+1=\left(x-2\right)^2+1>=1\forall x\) thỏa mãn ĐKXĐ
=>\(B=\dfrac{3}{x^2-4x+5}< =\dfrac{3}{1}=3\forall x\) thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi x-2=0
=>x=2
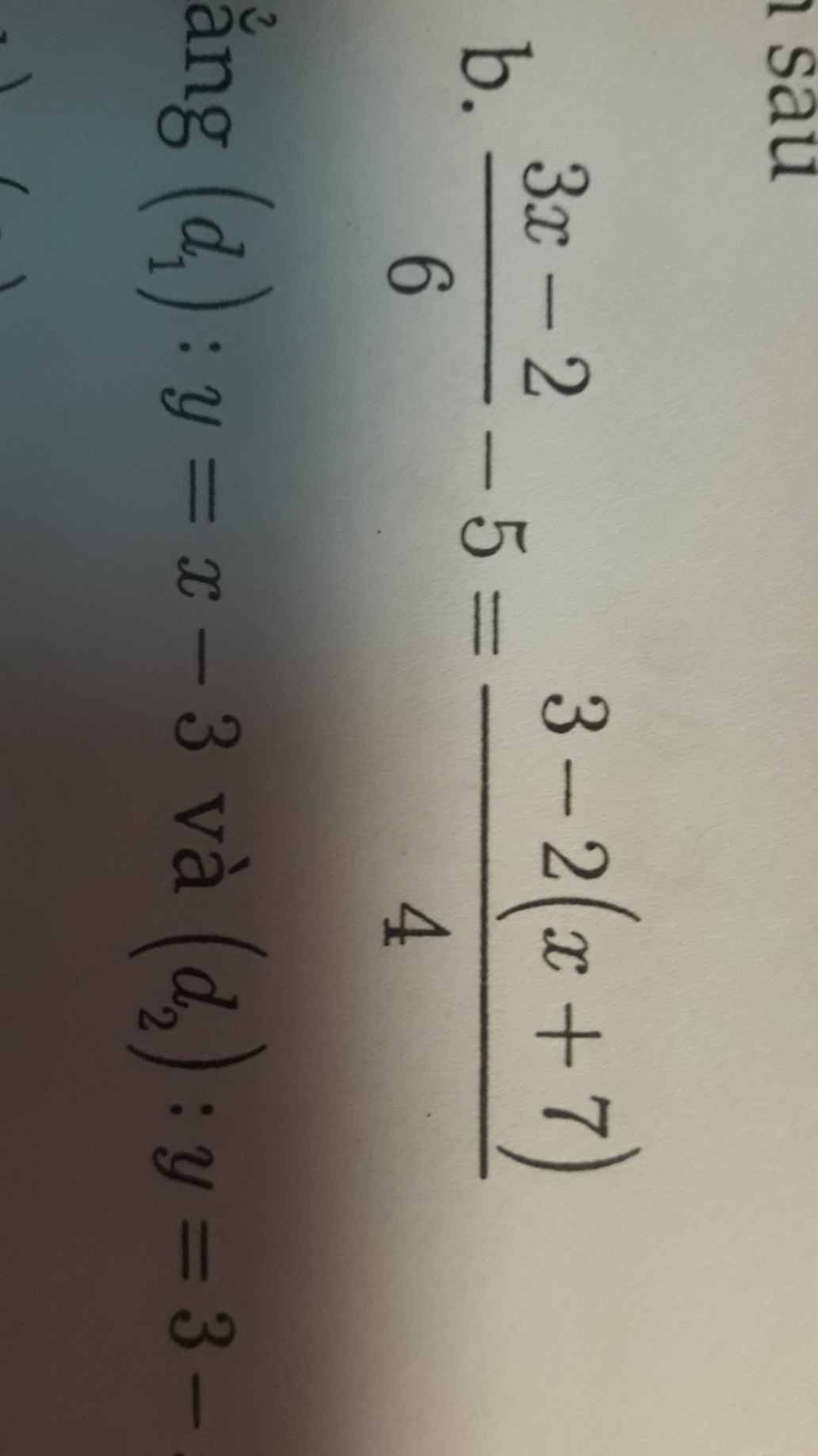

 mọi người giúp mình câu này với ạ
mọi người giúp mình câu này với ạ
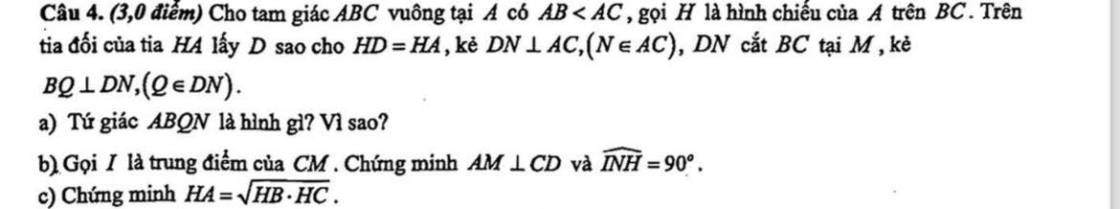
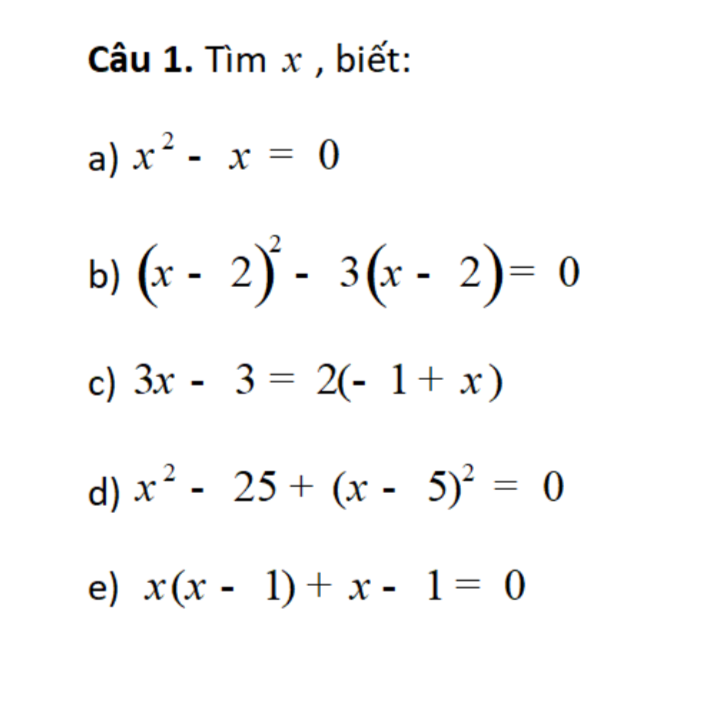


\(\dfrac{3x-2}{6}-5=\dfrac{3-2\left(x+7\right)}{4}\)
=>\(\dfrac{3x-32}{6}=\dfrac{3-2x-14}{4}\)
=>\(\dfrac{3x-32}{6}=\dfrac{-2x-11}{4}\)
=>2(3x-32)=3(-2x-11)
=>6x-64=-6x-33
=>12x=31
=>\(x=\dfrac{31}{12}\)