
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A= 2006 X 2008 - 20072
A = 2006 . 2008 - 2007 . 2007
A = 2006 . ( 2007 + 1 ) - 2007 . ( 2006 + 1 )
A = 2006 . 2007 + 2006 - 2007 . 2006 + 2007
A = -1
B= 2016 X 2018 - 20172
B= 2016 . 2018 - 2017 . 2017
B = 2016 . ( 2017 + 1 ) - 2017 . ( 2016 + 1 )
B = 2016 . 2017 + 2016 - 2017 . 2016 + 2017
B = -1

1)
\((x+2)(x+3)(x+4)(x+5)-24\\=[(x+2)(x+5)]\cdot[(x+3)(x+4)]-24\\=(x^2+7x+10)(x^2+7x+12)-24\)
Đặt \(x^2+7x+10=y\), khi đó biểu thức trở thành:
\(y(y+2)-24\\=y^2+2y-24\\=y^2+2y+1-25\\=(y+1)^2-5^2\\=(y+1-5)(y+1+5)\\=(y-4)(y+6)\\=(x^2+7x+10-4)(x^2+7x+10+6)\\=(x^2+7x+6)(x^2+7x+16)\)
2) Bạn xem lại đề!

Ta có : n^3 - n (n € Z )
= n(n^2 -1)
=n(n-1)(n+1)
=(n-1)n(n+1)
mà n-1 ; n ; n+1 là 3 số nguyên liên tiếp nên sẽ có 1 số chia hết cho 2 và một số chia hết cho 3
=> (n-1)n(n+1) chia hết cho 2 và 3
=> (n-1)n(n+1) chia hết cho 2.3
=> (n-1)n(n+1) chia hết cho 6 (đpcm)

4.42:
a:=>x+y=0 và y-1=0
=>y=1 và x=-1
b: =>x-5=0 và 2y-7=0
=>x=5 và y=7/2


10x(-4x-7)+8x(5x+5)= -60
=>-40x2-70x+40x2+40x=-60
=>-30x=-60
=>x=2


a: \(=\dfrac{x+2}{x+2}=1\)
b: \(=\dfrac{2x+6}{x+3}=2\)

Mình sẽ làm theo đề bài của mình nếu đúng thì ... nha
Biến đổi vế phải ta có :
( x + y) [ ( x - y)^2 + xy ] = ( x + y)( x^2 - 2xy + y^2 + xy)
= ( x+ y)( x^2 - xy+ y^2)
= x^3 + y^3
VẬy VT = VP đẳng thức được CM
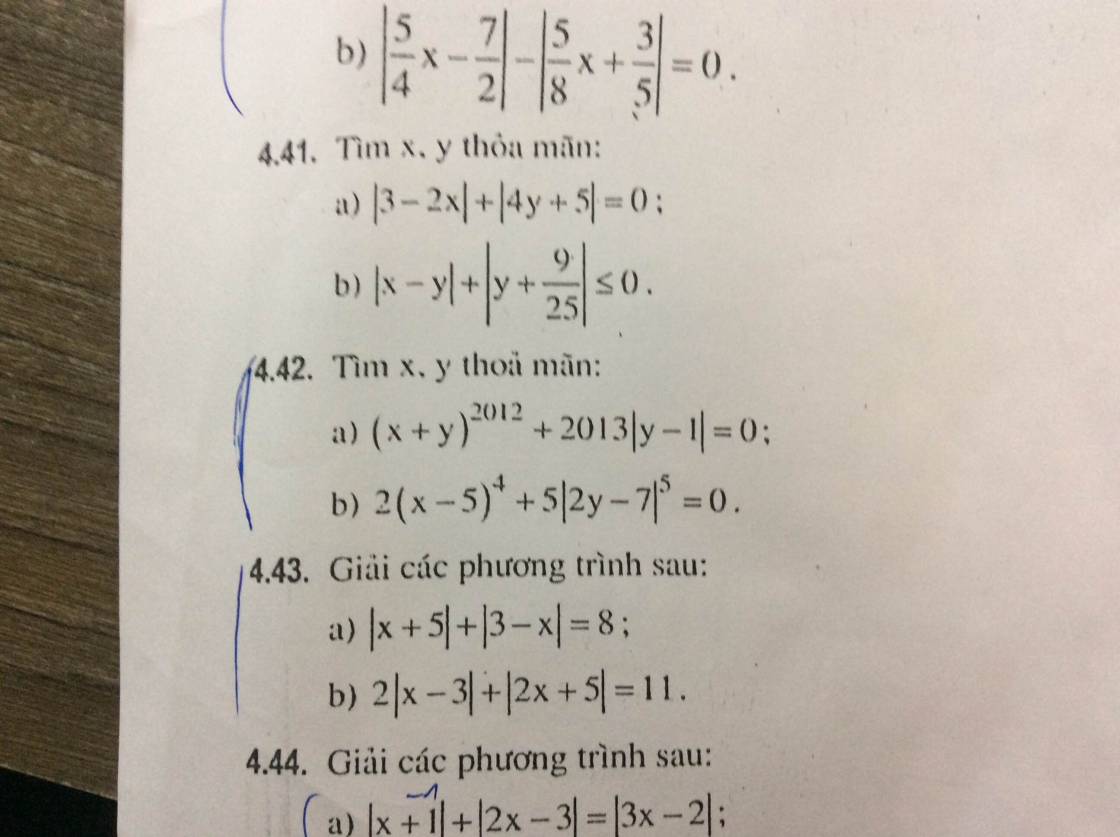
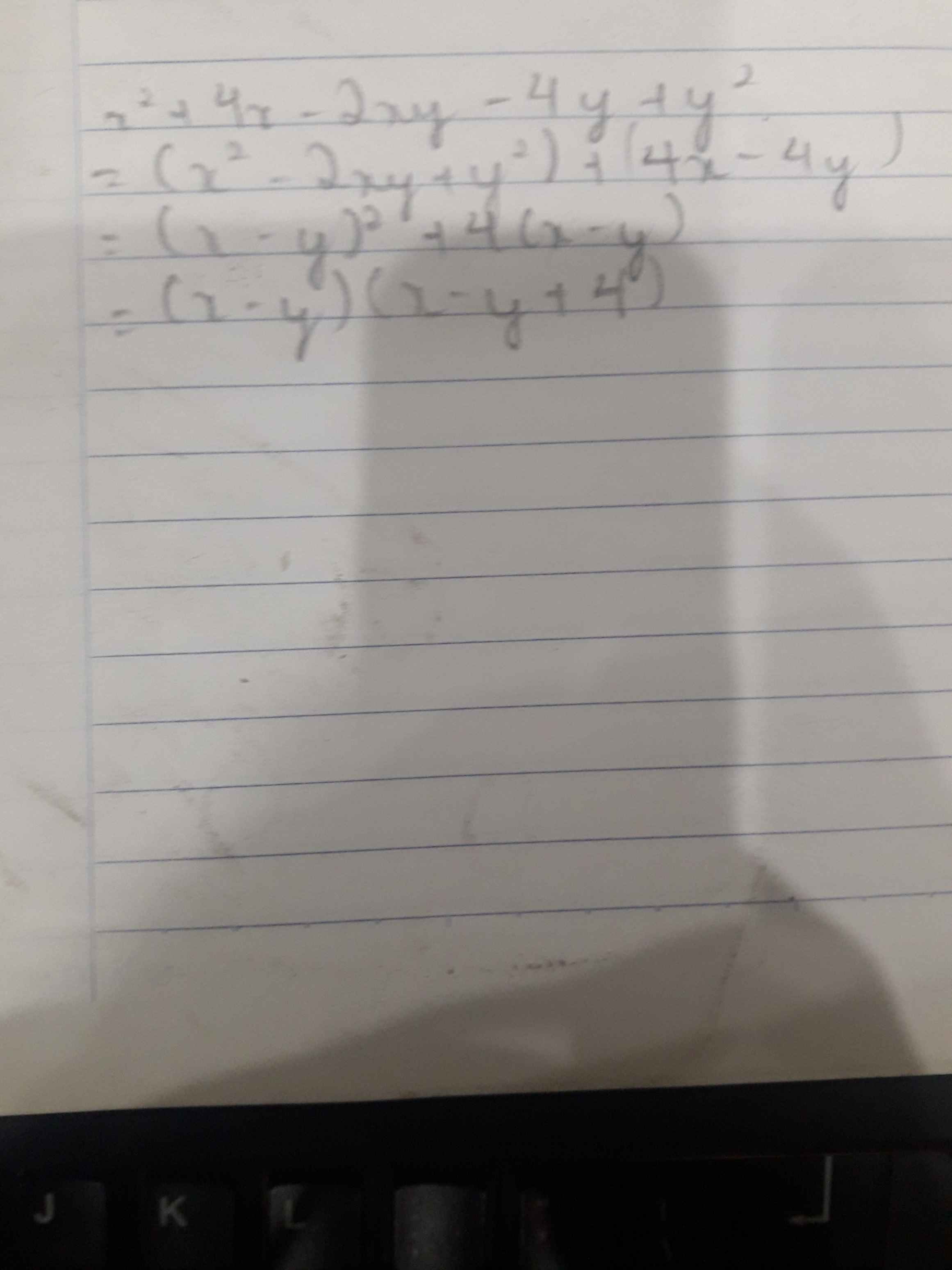
 mọi người giúp mình câu này với ạ
mọi người giúp mình câu này với ạ