K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
7 tháng 11 2021
a: \(\Leftrightarrow\left(3x-1\right)^4\cdot\left(3x-2\right)\cdot3x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=\dfrac{2}{3}\\x=0\end{matrix}\right.\)
1 tháng 11 2021
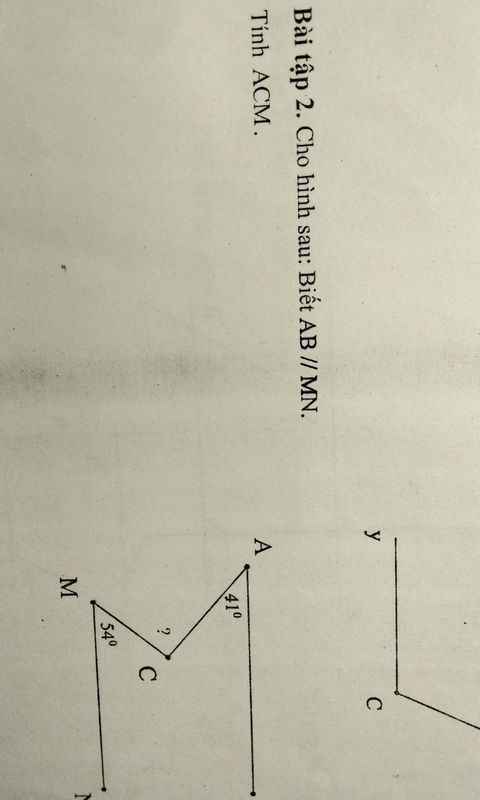
Kẻ CD//AB thì CD//MN
Do đó \(\widehat{ACD}=\widehat{CAB}=41^0;\widehat{MCD}=\widehat{CMN}=54^0\) (so le trong)
Vậy \(\widehat{ACM}=\widehat{ACD}+\widehat{DCM}=41^0+54^0=95^0\)
13 tháng 3 2022
a: Xét tứ giác ABKC có
I là trung điểm của AK
I là trung điểm của BC
Do đó: ABKC là hình bình hành
Suy ra: AB//KC
b: Xét ΔACK có CA=CK(=AB)
nên ΔACK cân tại C
PT
1
5 tháng 11 2021
\(=\dfrac{2^{15}\cdot3^8}{3^6\cdot2^6\cdot2^9}+\dfrac{9^3\cdot71}{3^2\cdot71}=3^2+81=90\)
KP
1
30 tháng 6 2023
2:
căn c+25=34
=>căn c=9
=>c=81
=>c^2-28=81^2-28=6533
3: xy-3x+y=14
=>x(y-3)+y-3=11
=>(y-3)(x+1)=11
=>(x+1;y-3) thuộc {(1;11); (11;1); (-1;-11); (-11;-1)}
=>(x,y) thuộc {(0;14); (10;4); (-2;-8); (-12;2)}
4:
TH1: AC=5cm
AB+AC<BC
=>Loại
TH2: AC=11cm
BC+AC>AB; BC+AB>AC; AB+AC>BC
=>Nhận
C ABC=11+11+5=27(cm)
BA
1
23 tháng 9 2021
Ta có: \(3x=4y\Rightarrow\dfrac{x}{4}=\dfrac{y}{3}\Rightarrow\dfrac{x}{20}=\dfrac{y}{15}\)
\(2y=5z\Rightarrow\dfrac{y}{5}=\dfrac{z}{2}\Rightarrow\dfrac{y}{15}=\dfrac{z}{6}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{20}=\dfrac{y}{15}=\dfrac{z}{6}=\dfrac{x+z}{20+6}=\dfrac{52}{26}=2\)
\(\Rightarrow\left\{{}\begin{matrix}x=20.2=40\\y=15.2=30\\z=6.2=12\end{matrix}\right.\)
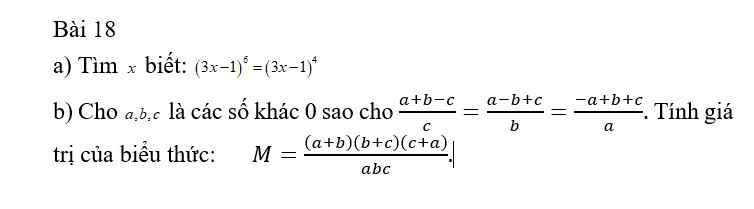
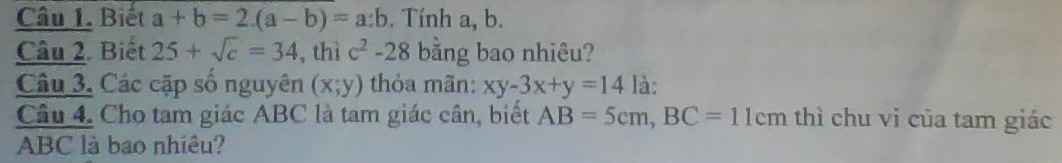
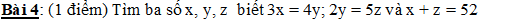
dụ thế dễ lừa lắm