
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



-Bài 3:
2) -Áp dụng BĐT Caushy Schwarz ta có:
\(A=\dfrac{1}{x^3+3xy^2}+\dfrac{1}{y^3+3x^2y}\ge\dfrac{\left(1+1\right)^2}{x^3+3xy^2+3x^2y+y^3}=\dfrac{4}{\left(x+y\right)^3}\ge\dfrac{4}{1^3}=4\)-Dấu "=" xảy ra khi \(x=y=\dfrac{1}{2}\)

\(1,\\ a,\dfrac{8x}{2xy}=\dfrac{4x}{y}\\ b,\dfrac{2xy}{6y}=\dfrac{x}{3}\\ c,\dfrac{3\left(x+2\right)}{2x}=\dfrac{6\left(x+2\right)}{4x}\\ d,\dfrac{4\left(x-2\right)}{3\left(x+1\right)}=\dfrac{8\left(x-2\right)x}{6\left(x+1\right)x}\\ 2,\\ \dfrac{x^2+3x+2}{x^2+x}=\dfrac{x^2+x+2x+2}{x\left(x+1\right)}=\dfrac{\left(x+1\right)\left(x+2\right)}{x\left(x+1\right)}=\dfrac{x+2}{x}\\ 3,\\ \dfrac{x^2-3x}{x^2-9}=\dfrac{x}{x+3}\)

Bài 3:
Ta có: \(x^2-2x+4=\left(x-1\right)^2+3\ge3\forall x\)
\(\Leftrightarrow P=\dfrac{15}{x^2-2x+4}=\dfrac{15}{\left(x-1\right)^2+3}\le5\forall x\)
Dấu '=' xảy ra khi x=1

Câu 1: A
Câu 2: B
Câu 3: D
Câu 4: A
Câu 5: C
Câu 6: B
Câu 7: A
Câu 9: B

a) \(\dfrac{A}{x-2}=\dfrac{x^2+3x+2}{x^2-4}\)
\(\Leftrightarrow\dfrac{A}{x-2}=\dfrac{\left(x+2\right)\left(x+1\right)}{\left(x-2\right)\left(x+2\right)}\)
\(\Leftrightarrow\dfrac{A}{x-2}=\dfrac{x+1}{x-2}\Leftrightarrow A=x+1\)
b) \(\dfrac{M}{x-1}=\dfrac{x^2+3x+2}{x+1}\)
\(\Leftrightarrow\dfrac{M}{x-1}=\dfrac{\left(x+1\right)\left(x+2\right)}{x+1}\)
\(\Leftrightarrow\dfrac{M}{x-1}=x+2\Leftrightarrow M=\left(x-1\right)\left(x+2\right)=x^2+x-2\)

Ta có:
(2 - 3x)(x + 8) = (3x - 2)(3 - 5x)
⇔ (2 - 3x)(x + 8) - (3x - 2)(3 - 5x) = 0
⇔ (2 - 3x)(x + 8) + (2 - 3x)(3 - 5x) = 0
⇔ (2 - 3x)(x + 8 + 3 - 5x) = 0
⇔ (2 - 3x)(11 - 4x) = 0
⇔ 2 - 3x = 0 hay 11 - 4x = 0
⇔ 2 = 3x hay 11 = 4x
⇔ x = \(\dfrac{2}{3}\) hay x = \(\dfrac{11}{4}\)
Vậy tập nghiệm của pt S = \(\left\{\dfrac{2}{3};\dfrac{11}{4}\right\}\)
<=> (2-3x ) (x+8) + (2-3x ) (3-5x)=0
<=> (2-3x ) ( x+8 + 3-5x ) =0
<=> (2-3x ) ( 11 - 4x ) = 0
=> 2-3x =0 hoặc 11-4x =0
3x = 2 4x =11
x = 2/3 x = 11/4



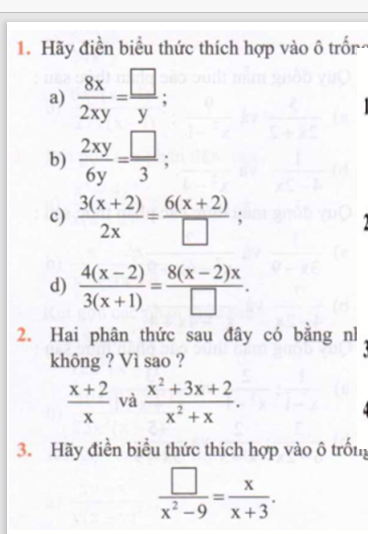 Mọi người giải giúp em với ạ em đang cần gấp ạ
Mọi người giải giúp em với ạ em đang cần gấp ạ Mọi người giải giúp em với ạ em đang cần gấp ạ
Mọi người giải giúp em với ạ em đang cần gấp ạ



 mọi người giải giúp em bài này với ạ em đang cần gấp ạ
mọi người giải giúp em bài này với ạ em đang cần gấp ạ
Câu 10: A
Câu 11: B
Câu 12: Chưa đủ cơ sở tính $\widehat{B}$, nhưng $\widehat{D}=110^0$
Câu 13: C
$BC=2DE=2.5=10$ (cm)
Câu 14: C
Câu 15: $MN=BC:2=8:2=4$ (cm)
Đáp án B.