Mọi người giúp em câu 4.3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CC
0
PQ
2
14 tháng 4 2021
a) Xét ΔMNI vuông tại M và ΔHPI vuông tại P có
\(\widehat{MIN}=\widehat{HIP}\)(hai góc đối đỉnh)
Do đó: ΔMNI\(\sim\)ΔHPI(g-g)
14 tháng 4 2021
b) Ta có: ΔMNI\(\sim\)ΔHPI(cmt)
nên \(\widehat{MNI}=\widehat{HPI}\)(hai góc tương ứng)
hay \(\widehat{MNI}=\widehat{MPK}\)
Xét ΔMNI vuông tại M và ΔMPK vuông tại M có
\(\widehat{MNI}=\widehat{MPK}\)(cmt)
Do đó: ΔMNI\(\sim\)ΔMPK(g-g)
Suy ra: \(\dfrac{MN}{MP}=\dfrac{MI}{MK}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(\dfrac{MN}{MI}=\dfrac{MP}{MK}\)
Xét ΔMNP vuông tại M và ΔMIK vuông tại M có
\(\dfrac{MN}{MI}=\dfrac{MP}{MK}\)(cmt)
Do đó: ΔMNP\(\sim\)ΔMIK(c-g-c)
7 tháng 4 2021
a) Xét ΔADH vuông tại H và ΔDBC vuông tại C có
\(\widehat{ADH}=\widehat{DBC}\)(hai góc so le trong, AD//BC)
Do đó: ΔADH\(\sim\)ΔDBC(g-g)
18 tháng 1 2022
a: \(=4x^2-x^4+8-2x^2=-x^4+2x^2+8\)
b: \(=\dfrac{x^2+x}{x+1}=x\)
RH
20 tháng 10 2021
a) x^2 - x = 0
x(x-1)=0
x=0 hoặc x=1
b) (x-2)^2 - 3(x-2)=0
(x-2)(x-5)=0
x=2 hoặc x=5
c) pt <=> 3(x - 1) - 2(x - 1)=0
<=> x-1=0
<=> x = 1
20 tháng 10 2021
a) \(\Rightarrow x\left(x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
b) \(\Rightarrow\left(x-2\right)\left(x-5\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=5\end{matrix}\right.\)
c) \(\Rightarrow3\left(x-1\right)-2\left(x-1\right)=0\)
\(\Rightarrow x-1=0\Rightarrow x=1\)
d) \(\Rightarrow\left(x-5\right)\left(x+5\right)+\left(x-5\right)^2=0\)
\(\Rightarrow\left(x-5\right).2x=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=5\end{matrix}\right.\)
e) \(\Rightarrow\left(x-1\right)\left(x+1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 4 2021
\(x^2+5y^2+2x-4xy-10y+14\)
\(=\left(x^2+4y^2+1-4xy+2x-4y\right)+\left(y^2-6y+9\right)+4\)
\(=\left(x-2y+1\right)^2+\left(y-3\right)^2+4>0\) ; \(\forall x;y\) (đpcm)
14 tháng 1 2023
a: Xét tứ giác AMCD có
I là trung điểm chung của AC và MD
góc AMC=90 độ
=>AMCD là hình chữ nhật
b: Xét tứ giác ABMD có
AD//BM
AD=BM
=>ABMD là hình bình hành
7 tháng 1 2022
Bài 1:
a: \(=-10x^3+20x^4-5x\)
b: \(=\dfrac{1}{3}a^2b+7a^5-1\)
c: \(=a^3+8+25-a^3=33\)
d: \(=x^2-16+8-x^3=-x^3+x^2-8\)
e: \(=a^3+1+8-a^3=9\)
f: \(=\dfrac{7-2x+4x-8}{2x+3}=\dfrac{2x-1}{2x+3}\)
g: \(=\dfrac{3}{2\left(x+3\right)}-\dfrac{2}{x\left(x+3\right)}\)
\(=\dfrac{3x-4}{2x\left(x+3\right)}\)
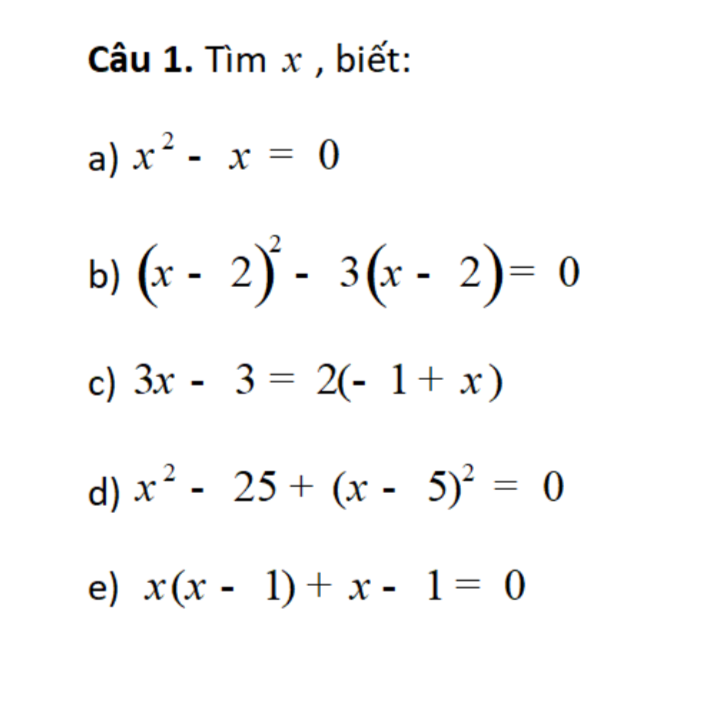
Bai 5 :
Theo giả thiết ta có : \(P=\frac{x\left(x+y+z\right)+yz}{y+z}+\frac{y\left(x+y+z\right)+zx}{z+x}+\frac{z\left(x+y+z\right)+xy}{x+y}\)
\(=\frac{x\left(x+y\right)+z\left(x+y\right)}{y+z}+\frac{y\left(y+z\right)+x\left(y+z\right)}{z+x}+\frac{z\left(y+z\right)+x\left(z+y\right)}{x+y}\)
\(=\frac{\left(x+y\right)\left(z+x\right)}{y+z}+\frac{\left(y+z\right)\left(x+y\right)}{z+x}+\frac{\left(z+x\right)\left(z+y\right)}{x+y}\)
Đặt \(\left\{x+y;y+z;z+x\right\}\rightarrow\left\{a;b;c\right\}\)bài toán quy về :
Cho \(\hept{\begin{cases}a+b+c=4\\a;b;c>0\end{cases}}\)Tìm GTNN của \(\frac{ac}{b}+\frac{ab}{c}+\frac{bc}{a}\)
Áp dụng bất đẳng thức AM-GM có :
\(\frac{ac}{b}+\frac{ab}{c}\ge2\sqrt{\frac{acab}{bc}}=2a\)
\(\frac{ab}{c}+\frac{bc}{a}\ge2\sqrt{\frac{abbc}{ca}}=2b\)
\(\frac{bc}{a}+\frac{ac}{b}\ge2\sqrt{\frac{bcac}{ab}}=2c\)
Cộng theo vế 3 bất đẳng thức cùng chiều ta được :
\(2\left(\frac{ac}{b}+\frac{bc}{a}+\frac{ab}{c}\right)\ge2\left(a+b+c\right)=2.4=8\)
\(< =>\frac{ac}{b}+\frac{bc}{a}+\frac{ab}{c}\ge\frac{8}{2}=4\)
Dấu "=" xảy ra khi và chỉ khi \(a=b=c=\frac{4}{3}< =>x=y=z=\frac{2}{3}\)
Vậy GTNN của P = 4 khi \(x=y=z=\frac{2}{3}\)
Kick mik nha