
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





4: Ta có: \(\sqrt{3+2\sqrt{2}}+\sqrt{6-4\sqrt{2}}\)
\(=\sqrt{2}+1+2-\sqrt{2}\)
=3
5: Ta có: \(2+\sqrt{17-4\sqrt{9}+4\sqrt{5}}\)
\(=2+\sqrt{5+4\sqrt{5}}\)
6: Ta có: \(2\sqrt{3}+\sqrt{2}+\sqrt{18-8\sqrt{2}}\)
\(=2\sqrt{3}+\sqrt{2}+4-\sqrt{2}\)
\(=4+2\sqrt{3}\)

Lời giải:
$\frac{x-2y}{3z}$ có thể nhận giá trị lớn nhất nếu $x$ lớn nhất và $y,z$ nhỏ nhất có thể.
$x$ lớn nhất có thể nhận là $14$ (theo điều kiện)
$y,z$ nhỏ nhất có thể nhận là $1,2$ (do $y,z$ phân biệt)
Nếu $x=14, y=1,z=2$ thì $\frac{x-2y}{3z}=2$
Nếu $x=14; y=2, z=1$ thì $\frac{x-2y}{3z}=\frac{10}{3}>2$
Đáp án D.

Bài 2:
a) Để hàm số đồng biến thì m+1>0
hay m>-1
b) Để hàm số đi qua điểm A(2;4) thì
Thay x=2 và y=4 vào hàm số, ta được:
\(\left(m+1\right)\cdot2=4\)
\(\Leftrightarrow m+1=2\)
hay m=1
c) Để hàm số đi qua điểm B(2;-4) thì
Thay x=2 và y=-4 vào hàm số, ta được:
\(2\left(m+1\right)=-4\)
\(\Leftrightarrow m+1=-2\)
hay m=-3
Bài 1:
b) Ta có: \(5\cdot\sqrt{25a^2}-25a\)
\(=5\cdot5\cdot\left|a\right|-25a\)
\(=-25a-25a=-50a\)

Bài 7:
Ta có: \(C=\dfrac{4+\sqrt{7}}{3\sqrt{2}+\sqrt{4+\sqrt{7}}}+\dfrac{4-\sqrt{7}}{3\sqrt{2}-\sqrt{4-\sqrt{7}}}\)
\(=\dfrac{\sqrt{2}\left(4+\sqrt{7}\right)}{6+\sqrt{8+2\sqrt{7}}}+\dfrac{\sqrt{2}\left(4-\sqrt{7}\right)}{6-\sqrt{8-2\sqrt{7}}}\)
\(=\dfrac{\sqrt{2}\left(4+\sqrt{7}\right)}{7+\sqrt{7}}+\dfrac{\sqrt{2}\left(4-\sqrt{7}\right)}{7-\sqrt{7}}\)
\(=\dfrac{\sqrt{2}\left(\sqrt{7}-1\right)\left(4+\sqrt{7}\right)}{6\sqrt{7}}+\dfrac{\sqrt{2}\left(\sqrt{7}+1\right)\left(4-\sqrt{7}\right)}{6\sqrt{7}}\)
\(=\dfrac{\sqrt{2}\left(-3+3\sqrt{7}+3+3\sqrt{7}\right)}{6\sqrt{7}}\)
\(=\sqrt{2}\)
6.
Ta có:
\(A=\sqrt{20+\sqrt{20+...+\sqrt{20}}}>\sqrt{20+\sqrt{\dfrac{1}{16}}}=\dfrac{9}{2}\)
\(B=\sqrt[3]{24+\sqrt[3]{24+...+\sqrt[3]{24}}}>\sqrt[3]{24}=\sqrt[3]{\dfrac{192}{8}}>\sqrt[3]{\dfrac{125}{8}}=\dfrac{5}{2}\)
\(\Rightarrow A+B>\dfrac{9}{2}+\dfrac{5}{2}=7\)
\(A=\sqrt[]{20+\sqrt[]{20+...+\sqrt[]{20}}}< \sqrt[]{20+\sqrt[]{20+...+\sqrt[]{25}}}=5\)
\(B=\sqrt[3]{24+\sqrt[3]{24+...+\sqrt[3]{24}}}< \sqrt[3]{24+\sqrt[3]{24+...+\sqrt[3]{27}}}=3\)
\(\Rightarrow A+B< 5+3=8\)









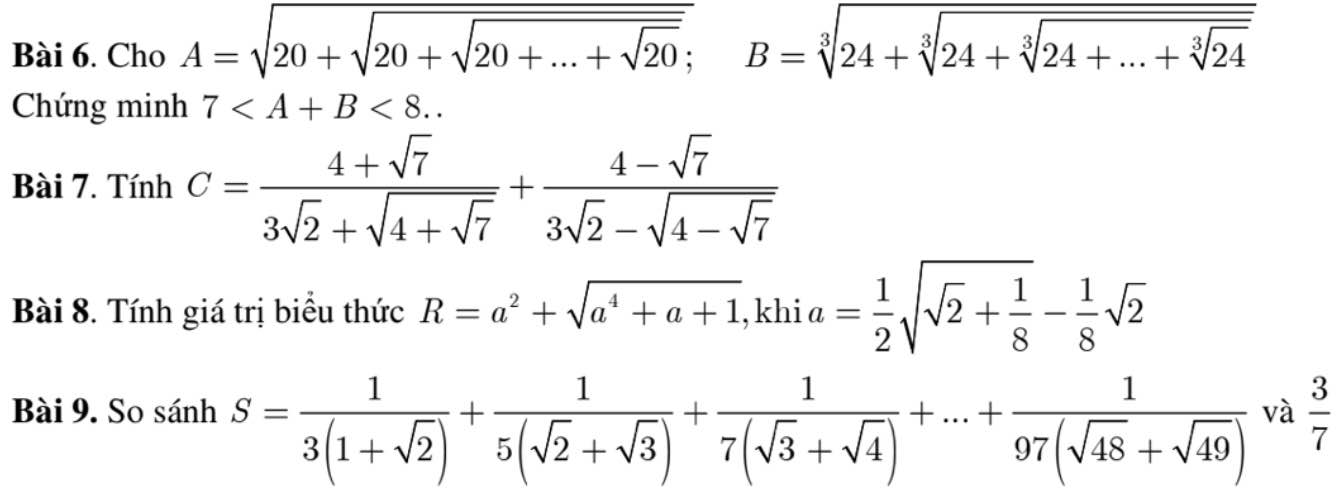
a) Hai đường tròn (O) và (O') cắt nhau tại A và B => OO' vuông góc AB
Xét đường tròn (O'): O'O vuông góc với dây AB, O nằm trên (O') => O là điểm chính giữa (AB
=> Sđ(OA = Sđ(OB => CO là phân giác ^BCD.
Xét tứ giác CHOD: CO là phân giác ^DCH (cmt), OD = OH, CH khác CD => CHOD nội tiếp.
b) Ta thấy:
AB là trục đẳng phương của (O) và (O')
CO là trục đẳng phương của (O') và (CHOD)
DH là trục đẳng phương của (CHOD) và (O)
Suy ra AB,CO,DH đồng quy tại I.
c) Lấy P và Q' trên (O) sao cho CP, CQ' tiếp xúc với (O), PQ' cắt CD và CB tại U,V; CO cắt (O) tại G,K
Ta có \(\left(CUAD\right)=-1=\left(CVBH\right)\)=> AB,DH,PQ' đồng quy => PQ' cắt CO tại I
Suy ra \(\left(CIKG\right)=-1\), vì O là trung điểm KG nên \(\overline{CI}.\overline{CO}=\overline{CK}.\overline{CG}\)(Maclaurin)
Mà \(CQ^2=CI.CO\)nên \(CQ^2=\overline{CK}.\overline{CG}=P_{C/\left(O\right)}\). Vậy CQ tiếp xúc với (O).
d) Gọi AF giao TD tại J.
Ta thấy: ^JNE = ^AEO (Cùng phụ ^DEN), ^NEJ = ^EOA vì J là trực tâm \(\Delta\)EAT và ^NEJ, ^EOA cùng phụ ^OEJ
=> \(\Delta\)ENJ ~ \(\Delta\)OEA. Tương tự \(\Delta\)EMJ ~ \(\Delta\)OET
=> \(\frac{EN}{OE}=\frac{EJ}{OA}=\frac{EJ}{OT}=\frac{EM}{OE}\). Vậy EM = EN.