KL
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
KL
3
KL
6 tháng 9 2021
\(\orbr{\frac{1}{1-\sqrt{x}}-\frac{1}{\sqrt{x}}]}\div\orbr{\begin{cases}\\\end{cases}(2\sqrt{x}-1)(\frac{1}{1-\sqrt{x}}+\frac{\sqrt{x}}{1-\sqrt{x}+x})]}\)
sori mng em bị lag xíu
HK
1
NV
5
8 tháng 9 2021
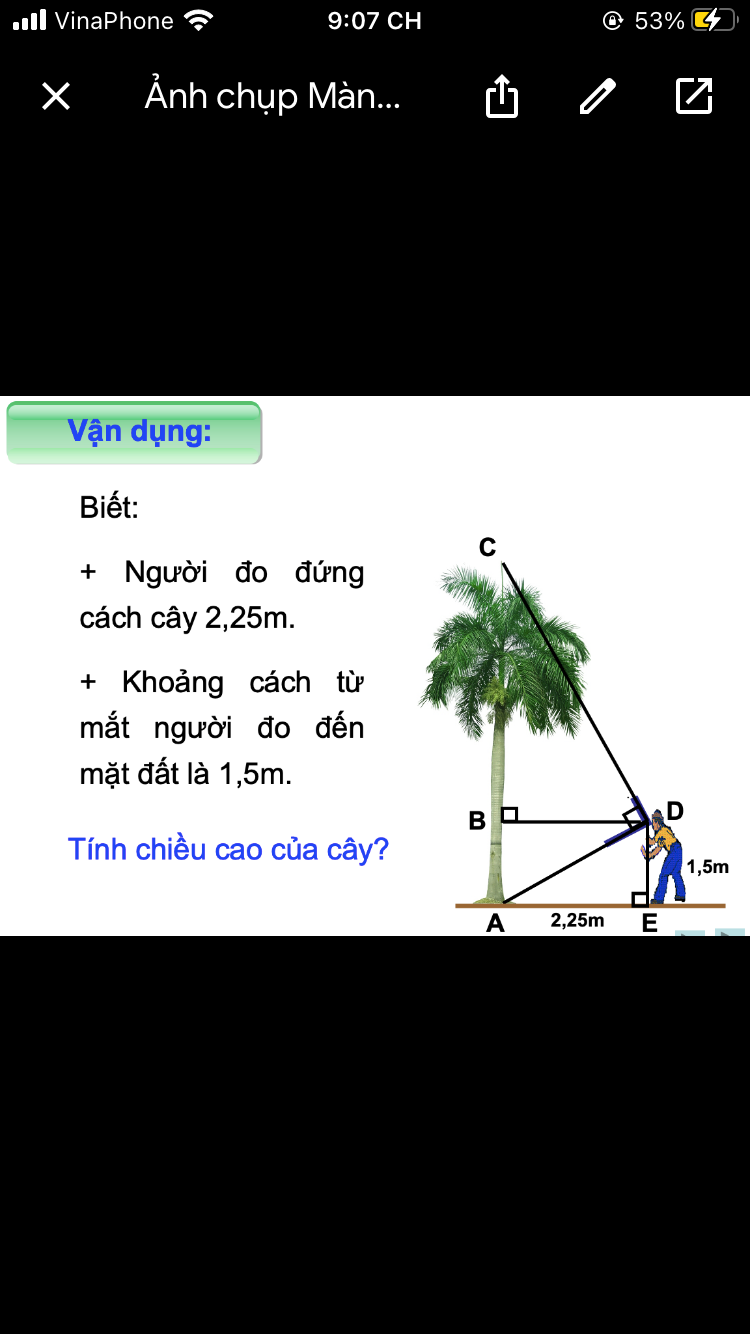
Xét tam giác ADE vuông tại E có:
\(AD^2=AE^2+DE^2\)(định lý Pytago)
\(\Rightarrow AD^2=\dfrac{117}{16}\left(m\right)\)
Xét tam giác ADC vuông tại D có đường cao DB có:
\(AD^2=AB.AC\)(hệ thức lượng trong tam giác vuông)
\(\Rightarrow AC=\dfrac{AD^2}{AB}=\dfrac{117}{16}:1,5=\dfrac{39}{8}\left(m\right)\)
Vậy chiều cao của cây là \(\dfrac{39}{8}m\)
21 tháng 8 2021
Bài 1:
a: Xét tứ giác NPIK có
\(\widehat{NKP}=\widehat{NIP}\left(=90^0\right)\)
Do đó: NPIK là tứ giác nội tiếp
hay N,P,I,K cùng thuộc 1 đường tròn
b: Xét tứ giác MKHI có
\(\widehat{MKH}+\widehat{MIH}=180^0\)
Do đó: MKHI là tứ giác nội tiếp
hay M,K,H,I cùng thuộc 1 đường tròn
YN
2
8 tháng 8 2023
Bạn tải ảnh về máy, vào biểu tượng 
để đăng ảnh lên CH nhé.
NV
3
AH
Akai Haruma
Giáo viên
11 tháng 8 2021
Bài 4:
a. ĐKXĐ: \(\left\{\begin{matrix} x-1\geq 0\\ x-1\neq 2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq 1\\ x\neq 3\end{matrix}\right.\)
b. \(B=\frac{x-3}{\frac{x-1-2}{\sqrt{x-1}+\sqrt{2}}}=\sqrt{x-1}+\sqrt{2}\)
\(x=4(2-\sqrt{3})\Rightarrow x-1=7-4\sqrt{3}=(2-\sqrt{3})^2\)
\(\Rightarrow \sqrt{x-1}=2-\sqrt{3}\Rightarrow B=\sqrt{x-1}+\sqrt{2}=2-\sqrt{3}+\sqrt{2}\)
c.
$\sqrt{x-1}\geq 0$ với mọi $x\geq 1; x\neq 3$
$\Rightarrow B=\sqrt{x-1}+\sqrt{2}\geq \sqrt{2}$
Vậy $B_{\min}=\sqrt{2}$ khi $x=1$
AH
Akai Haruma
Giáo viên
11 tháng 8 2021
Bài 5:
\(C=\frac{x-2\sqrt{xy}+y+4\sqrt{xy}}{\sqrt{x}+\sqrt{y}}-\frac{\sqrt{xy}(\sqrt{x}-\sqrt{y})}{\sqrt{xy}}\)
\(=\frac{(\sqrt{x}+\sqrt{y})^2}{\sqrt{x}+\sqrt{y}}-(\sqrt{x}-\sqrt{y})=(\sqrt{x}+\sqrt{y})-(\sqrt{x}-\sqrt{y})\)
\(=2\sqrt{y}\) vẫn phụ thuộc vào biến $y$ bạn ạ. Bạn xem lại đề.
30 tháng 8 2021
7)
\(=\dfrac{\left(5-\sqrt{5}\right).\left(1+\sqrt{5}\right)}{\left(1-\sqrt{5}\right)\left(1+\sqrt{5}\right)}+\dfrac{3\left(\sqrt{2}+\sqrt{5}\right)}{\left(\sqrt{2}-\sqrt{5}\right)\left(\sqrt{2}+\sqrt{5}\right)}\)
\(=\dfrac{\left(5-\sqrt{5}\right)\left(1+\sqrt{5}\right)}{1-5}+\dfrac{3\left(\sqrt{2}+\sqrt{5}\right)}{4-5}\)
\(=\dfrac{5+5\sqrt{5}-\sqrt{5}-5}{4}+3\left(\sqrt{2}+\sqrt{5}\right)\)
=\(\dfrac{4\sqrt{5}}{4}+3\left(\sqrt{2}+\sqrt{5}\right)\)
\(=\sqrt{5}+3\sqrt{2}+3\sqrt{5}\)
\(=4\sqrt{5}+3\sqrt{2}\)
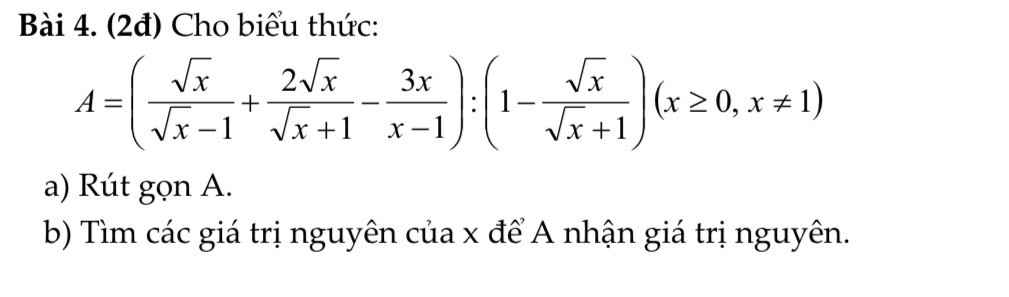
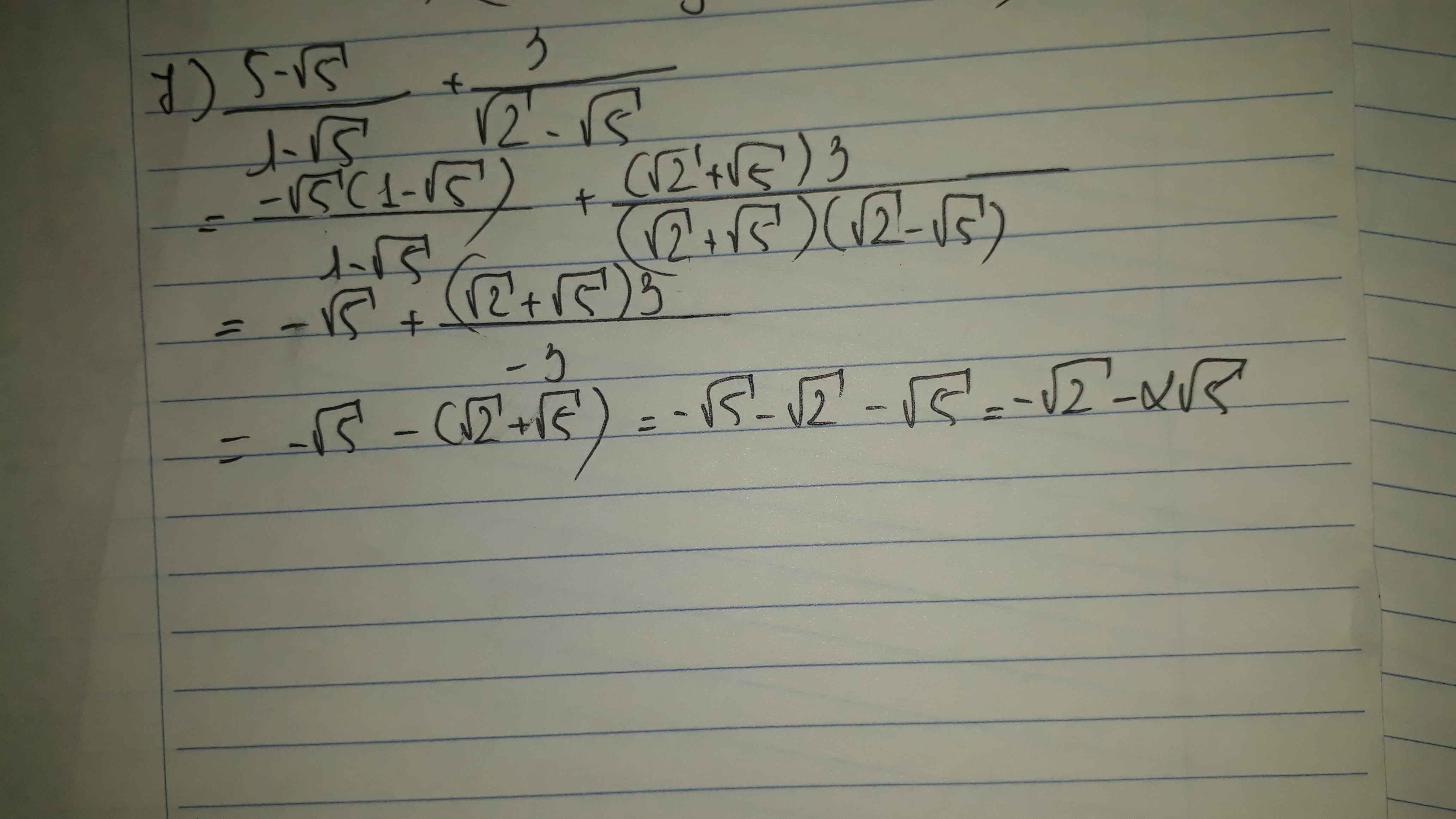
Bài 3.
\(P=\left(\frac{1}{1-\sqrt{x}}-\frac{1}{\sqrt{x}}\right)\div\left[\left(2\sqrt{x}-1\right)\left(\frac{1}{1-\sqrt{x}}+\frac{\sqrt{x}}{1-\sqrt{x}+x}\right)\right]\)
\(=\frac{\sqrt{x}-1+\sqrt{x}}{\sqrt{x}-x}\div\left[\left(2\sqrt{x}-1\right)\left(\frac{1}{1-\sqrt{x}}+\frac{\sqrt{x}}{1-\sqrt{x}+x}\right)\right]\)
\(=1\div\left(\frac{\sqrt{x}-x}{1-\sqrt{x}}+\frac{\sqrt{x}\left(\sqrt{x}-x\right)}{1-\sqrt{x}+x}\right)\)
\(=1\div\left(\sqrt{x}+\frac{x-x\sqrt{x}}{x-\sqrt{x}+1}\right)\)
\(=1\div\frac{\sqrt{x}}{x-\sqrt{x}+1}=\frac{x-\sqrt{x}+1}{\sqrt{x}}\)