CC
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CC
1
16 tháng 9 2021
\(\left(10-2n\right)⋮\left(n-2\right)\)
\(\Rightarrow-2\left(n-2\right)+6⋮\left(n-2\right)\)
\(\Rightarrow\left(n-2\right)\inƯ\left(6\right)=\left\{1;-1;2;-2;3;-3;6;-6\right\}\)
\(\Rightarrow n\in\left\{3;1;4;0;5;1;8;-4\right\}\)
27 tháng 1 2021
a, \(2n+5⋮n-1\)
\(2\left(n-1\right)+7⋮n-1\)
\(7⋮n-1\)hay \(n-1\inƯ\left(7\right)=\left\{\pm1;\pm7\right\}\)
| n - 1 | 1 | -1 | 7 | -7 |
| n | 2 | 0 | 8 | -6 |
b, Công thức tổng quát : \(A\left(x\right).B\left(x\right)=0\Rightarrow\orbr{\begin{cases}A\left(x\right)=0\\B\left(x\right)=0\end{cases}}\)
\(\left(2n+3\right)\left(n-4\right)=0\Leftrightarrow\orbr{\begin{cases}n=-\frac{3}{2}\\n=4\end{cases}}\)
c, \(\left|x-3\right|< 3\Leftrightarrow-3< x-3< 3\)
\(\Leftrightarrow-3+3< x< 3+3\Leftrightarrow0< x< 6\)
Vậy \(x\in\left\{1;2;3;4;5;\right\}\)
9 tháng 9 2021
\(\left(3x-4\right)^3=5^2+4.5^2\)
\(\Leftrightarrow\left(3x-4\right)^3=5^2\left(1+4\right)\)
\(\Leftrightarrow\left(3x-4\right)^3=5^3\)
\(\Leftrightarrow3x-4=5\Leftrightarrow3x=9\Leftrightarrow x=3\)
9 tháng 9 2021
Ta có: \(\left(3x-4\right)^3=5^2+4\cdot5^2\)
\(\Leftrightarrow3x-4=5\)
hay x=3
AH
Akai Haruma
Giáo viên
4 tháng 9 2021
Lời giải:
$A=7+(7^2+7^3+7^4+7^5)+(7^6+7^6+7^8+7^9)+....+(7^{2018}+7^{2019}+7^{2020}+7^{2021})$
$=7+7^2(1+7+7^2+7^3)+7^6(1+7+7^2+7^3)+....+7^{2018}(1+7+7^2+7^3)$
$=7+(1+7+7^2+7^3)(7^2+7^6+....+7^{2018}$
$=7+400(7^2+7^6+....+7^{2018})$
Dễ thấy $400(7^2+7^6+....+7^{2018})$ tận cùng là $0$
Do đó $A$ tận cùng là $7$
12 tháng 9 2021
\(3\left(x+2\right)^3-1^{2019}=5\cdot4^2\)
\(\Leftrightarrow3\left(x+2\right)^3=5\cdot16+1=81\)
\(\Leftrightarrow x+2=3\)
hay x=1
MH
12 tháng 9 2021
\(4^{15}.9^{15}< 2^n.3^n< 18^{16}.2^{16}\)
⇒\(\left(4.9\right)^{15}< \left(2.3\right)^n< \left(18.2\right)^{16}\)
⇒\(\left(6^2\right)^{15}< 6^n< \left(6^2\right)^{16}\)
⇒\(6^{30}< 6^n< 6^{32}\)
⇒\(6^n=6^{31}\)
⇒n=31
12 tháng 9 2021
\(4^{15}\cdot9^{15}< 2^n\cdot3^n< 18^{16}\cdot2^{16}\\ \Leftrightarrow\left(4\cdot9\right)^{15}< \left(2\cdot3\right)^n< \left(18\cdot2\right)^{16}\\ \Leftrightarrow36^{15}< 6^n< 36^{16}\\ \Leftrightarrow6^{30}< 6^n< 6^{32}\\ \Leftrightarrow n=31\)
NN
0
HV
1
2 tháng 11 2021
a) \(2C=2^2+2^3+...+2^{101}\)
\(\Rightarrow C=2C-C=2^2+2^3+...+2^{101}-2-2^2-...-2^{100}=2^{101}-2\)
\(\Rightarrow2^{2x-1}-2=2^{101}-2\Rightarrow2x-1=101\Rightarrow2x=102\Rightarrow x=51\)
b) \(\Rightarrow3\left(x-2\right)+7⋮\left(x-2\right)\)
\(\Rightarrow\left(x-2\right)\inƯ\left(7\right)=\left\{-7;-1;1;7\right\}\)
\(\Rightarrow x\in\left\{-5;1;3;9\right\}\)
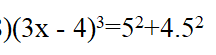
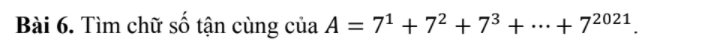
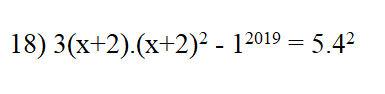
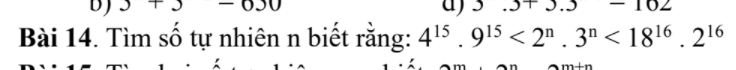
BN THAM KHẢO:
Lời giải 1:10−2n⋮n−210−2n⋮n−2
⇔2n−10⋮n−2⇔2n−10⋮n−2
⇔2(n−2)−6⋮n−2⇔2(n−2)−6⋮n−2
⇔6⋮n−2⇔6⋮n−2
Ta có bảng
Vậy n∈{−4;−1;0;1;3;4;5;8}
Lời giải 2:
Ta có :
10-2n = -2n+10 = -2n+4 + 6 = -2.(n-2) + 6
Vì -2.(n-2) chia hết cho n-2
=> để 10-2n chia hết cho n-2
=> 6 chia hết cho n - 2
=> n-2 ∈ Ư(6) = {-1;1;2;-2;3;-3;6;-6}
=> n ∈ {1;3;4;0;5;-1;8;-4}
BN CHỌN CÁCH NÀO CŨNG ĐC!