K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
giúp mk với, mk cần gấp, mn nêu cả lời giải chi tiêt 1 chút giúp mk nhé, cam on mn rất nhìu ạ
1 tháng 11 2021
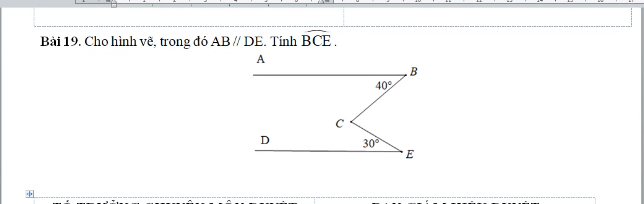
Kẻ CF//AB thì CF//DE
Do đó \(\widehat{BCF}=\widehat{ABC}=40^0;\widehat{FCE}=\widehat{CED}=30^0\) (so le trong)
Vậy \(\widehat{BCE}=\widehat{BCF}+\widehat{FCE}=30^0+40^0=70^0\)
giúp mk với mn mk đang gấp
22 tháng 12 2021
Câu 5:
Ta thấy \(\left(x-2\right)^2\ge0\Rightarrow A\ge-1\)
Dấu "=" xảy ra khi \(\left(x-2\right)^2=0\Leftrightarrow x-2=0\Leftrightarrow x=2\)
7N
giúp mk với, mk cần gấp ạ. camon mn rất nhìu, giải chi tiết dễ hiểu giúp mk nha
0
giúp mk với mn ơi
2 tháng 11 2021
a) Ta có: a⊥m,b⊥m
=> a//b
b) Ta có: a//b
\(\Rightarrow\widehat{D_1}=\widehat{xBD}=60^0\)(so le trong)
\(\Rightarrow\widehat{D_1}=\widehat{D_2}=60^0\)(đối đỉnh)
c) Ta có: a//b
\(\Rightarrow\widehat{ABD}=\widehat{CDE}\)(đồng vị)
\(\Rightarrow\dfrac{1}{2}\widehat{ABD}=\dfrac{1}{2}\widehat{CDE}\)
\(\Rightarrow\widehat{DBt}=\widehat{EDy}\)
Mà 2 góc này đồng vị
=> Bt//Dy
2
16 tháng 5 2022
`R(x)=P(x)-Q(x)`
`=x^3-x^2+x-x^2+2x^2=x^2+x`
Cho `R(x)=0`
`=>x^2+x=0`
`=>x(x+1)=0`
`@TH1:x=0`
`@TH2:x+1=0=>x=-1`
`->C`
28 tháng 7 2023
e: Xét ΔBMA vuông tại M và ΔBMK vuông tại M có
BM chung
góc ABM=góc KBM
=>ΔBMA=ΔBMK
f: Xét ΔBAE và ΔBKE có
BA=BK
góc ABE=góc KBE
BE chung
=>ΔBAE=ΔBKE
=>góc BKE=90 độ
=>EK vuông góc BC
g: AE=EK
EK<EC
=>AE<EC
h: góc NAK+góc BKA=90 độ
góc CAK+góc BAK=90 độ
mà góc BKA=góc BAK
nên góc NAK=góc CAK
=>AK là phân giác của góc CAN
7N
1
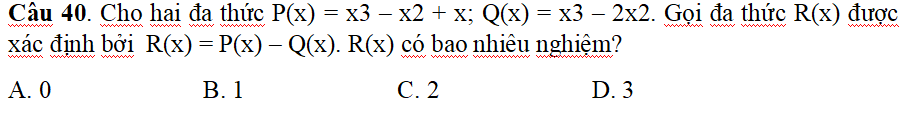
a) Xét tam giác OAD và tam giác OBC có:
OA = OB (gt).
^O chung.
OD = OC (gt).
=> Tam giác OAD = Tam giác OBC (c - g - c).
b) Tam giác OAD = Tam giác OBC (cmt).
=> ^OAD = ^OBC (cặp cạnh tương ứng).
Mà : ^OAD + ^CAD = 180;
^OBC + ^CBD = 180o.
=> ^CAD = ^CBD.