PM
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 2 2020
Câu a làm rồi
Câu b hình như bạn nhầm đề, với dạng của dãy như vậy thì số hạng tổng quát của nó là \(n\left(3n-1\right)\) chứ ko phải \(n\left(3n+1\right)\)
\(\sum n\left(3n-1\right)=3\sum n^2-\sum n=\frac{n\left(n+1\right)\left(2n+1\right)}{2}-\frac{n\left(n+1\right)}{2}=\frac{n\left(n+1\right)}{2}\left(2n-1-1\right)=n^2\left(n+1\right)\)
NP
1
HT
20 tháng 12 2020
Tui làm theo cách tiểu học, để mai nghĩ xem có cách nào làm "cấp 3" ko
2+3=5; 5+3=8
Số số hạng: \(\dfrac{3n-1-2}{3}+1=n\left(so-hang\right)\)
Tổng: \(\dfrac{\left(3n-1+2\right).n}{2}=\dfrac{n\left(3n+1\right)}{2}\)
PT
1
CM
20 tháng 10 2017
Chứng minh: 3n > 3n + 1 (1)
+ Với n = 2 thì (1) ⇔ 9 > 7 (luôn đúng).
+ Giả sử (1) đúng với n = k ≥ 2, tức là 3k > 3k + 1.
Ta chứng minh đúng với n= k+1 tức là chứng minh: 3k+ 1 > 3(k+1) + 1
Thật vậy, ta có:
3k + 1 = 3.3k > 3.(3k + 1) (Vì 3k > 3k + 1 theo giả sử)
= 9k + 3
= 3k + 3 + 6k
= 3.(k + 1) + 6k
> 3(k + 1) + 1.( vì k ≥ 2 nên 6k ≥ 12> 1)
⇒ (1) đúng với n = k + 1.
Vậy 3n > 3n + 1 đúng với mọi n ≥ 2.
MH
9 tháng 4 2017
a) Dễ thấy bất đẳng thức đúng với n = 2
Giả sử bất đẳng thức đúng với n = k ≥ 2, tức là
3k > 3k + 1
Nhân hai vế của (1) vơi 3, ta được:
3k + 1 > 9k + 3 <=> 3k + 1 > 3k + 4 + 6k -1.
Vì 6k - 1 > 0 nên
3k + 1 > 3k + 4 hay 3k + 1 > 3(k + 1) + 1.
tức là bất đẳng thức đúng với n = k + 1.
Vậy 3n > 3n + 1 với mọi số tự nhiên n ≥ 2.
b) Với n = 2 thì vế trái bằng 8, vế phải bằng 7. Vậy bất đẳng thức đúng với n = 2
Giả sử bất đẳng thức đúng với n = k ≥ 2, tức là
2k + 1 > 2k + 3 (2)
Ta phải chứng minh nó cũng đúng với n= k + 1, nghĩa là phải chứng minh
2k + 2 > 2(k + 1) + 3 <=> 2k + 2 > 2k + 5
Nhân hai vế của bất đẳng thức (2) với 2, ta được:
2k + 2 > 4k + 6 <=> 2k + 2 > 2k +5 + 2k + 1.
Vì 2k + 1> 0 nên 2k + 2 > 2k + 5
Vậy 2n + 1 > 2n + 3 với mọi số tự nhiên n ≥ 2.
PT
1
NP
1
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 2 2020
\(\sum n\left(3n+1\right)=\sum3n^2+\sum n=3\sum n^2+\sum n\)
\(=\frac{n\left(n+1\right)\left(2n+1\right)}{2}+\frac{n\left(n+1\right)}{2}=\frac{n\left(n+1\right)}{2}\left(2n+1+1\right)=n\left(n+1\right)^2\)
7 tháng 7 2022
\(=n\left(2n^2-2n-n+1\right)\)
\(=n\left(n-1\right)\left(2n-1\right)\)
TH1: n=3k
\(A=3k\left(3k-1\right)\left(6k-1\right)⋮3\)
mà A luôn chia hết cho 2(do n;n-1 là hai số liên tiếp)
nên A chia hết cho 6
TH2: n=3k+1
\(A=\left(3k+1\right)\left(3k+1-1\right)\left(6k+2-1\right)\)
\(=\left(3k+1\right)\left(3k\right)\cdot\left(6k+1\right)⋮3\)
=>A chia hết cho 6
TH3: n=3k+2
\(A=\left(3k+2\right)\left(3k+1\right)\left(6k+4-1\right)\)
\(=\left(3k+2\right)\left(3k+1\right)\left(6k+3\right)⋮6\)
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 4 2019
Nhìn quen quen, có phải nó đây ko bạn?
Câu hỏi của Nguyễn Lê Nhật Linh - Toán lớp 11 | Học trực tuyến
Tìm trong CHTT chứ mình cũng ko nhớ là đã làm rồi :))
28 tháng 4 2019
(b)=b(b−c)(b−a)f(b)=b(b−c)(b−a)
f(c)=c(c−a)(c−b)f(c)=c(c−a)(c−b)
Lại có f(a).f(b).f(c)=−abc(a−b)2(b−c)2(c−a)2f(a).f(b).f(c)=−abc(a−b)2(b−c)2(c−a)2
Vì vậy tồn tại 1 trong 3 số đó âm hay phương trình luôn có nghiệm.
Do hệ số A của pt dương
Nên:
a.f(α)<0a.f(α)<0 thì pt luôn có nghiệm thỏa x1<α<x2x1<α<x2
8 tháng 12 2021
tham khảo:
\(a) 2+5+8+...+(3n−1)=n(3n+1)2 (1) Đặt Sn=2+5+8+...+(3n−1) Với n=1 ta có: S1=2=1(3.1+1)2 Giả sử (1) đúng với n=k(k≥1), tức là Sk=2+5+8+...+(3k−1)=k(3k+1)2 Ta chứng minh (1) đúng với n=k+1 hay Sk+1=(k+1)(3k+4)2 Thật vậy ta có: Sk+1=2+5+8+...+(3k−1)+[3(k+1)−1]=Sk+3k+2=k(3k+1)2+3k+2=3k2+k+6k+42=3k2+7k+42=(k+1)(3k+4)2 Vậy (1) đúng với mọi k≥1 hay (1) đúng với mọi n∈N∗ b) 3+9+27+...+3n=12(3n+1−3) (2) Đặt Sn=3+9+27+...+3n=12(3n+1−3) Với n=1, ta có: S1=3=12(32−3) (hệ thức đúng) Giả sử (2) đúng với n=k(k≥1) tức là Sk=3+9+27+...+3k=12(3k+1−3) Ta chứng minh (2) đúng với n=k+1, tức là chứng minh Sk+1=12(3k+2−3) Thật vậy, ta có: Sk+1=3+9+27+...+3k+1=Sk+3k+1=12(3k+1−3)+3k+1=32.3k+1−32=12(3k+2−3)(đpcm) Vậy (2) đúng với mọi k≥1 hay đúng với mọi n∈N∗\)
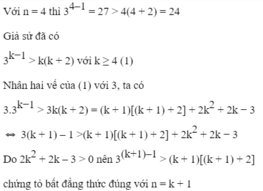
Ta có:
3n = Ba n = Bố N = Bốn = 4 .....
Vậy 3n = 4 ( với mọi n )
~ Hk T ~
3n = 4 vì:
3n hay Ba n => Bố n = 4